
【题目】某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈ ![]() ,tan48°≈
,tan48°≈ ![]() ,sin64°≈
,sin64°≈ ![]() ,tan64°≈2)
,tan64°≈2)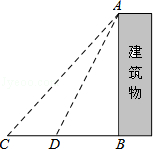
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2 , 当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.. 计算题:
(1)8﹣(﹣10)﹣|﹣2|
(2)2 ![]() ﹣3
﹣3![]() +(﹣3
+(﹣3![]() )﹣(+5
)﹣(+5![]() )
)
(3)﹣24×(﹣ ![]() +
+![]() ﹣
﹣![]() )
)
(4)﹣49 ![]() ×10(简便运算)
×10(简便运算)
(5)﹣ ![]() ÷(
÷(![]() ﹣
﹣![]() +
+![]() )
)
(6)3×(﹣38 ![]() )﹣4×(﹣38
)﹣4×(﹣38 ![]() )﹣38
)﹣38![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB∥CD,点P为定点,E、F分别是AB、CD上的动点.
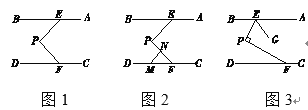
(1)求证:∠P=∠BEP+∠PFD;
(2)若点M为CD上一点,如图2,∠FMN=∠BEP,且MN交PF于N.试说明∠EPF与∠PNM的数量关系,并证明你的结论;
(3)移动E、F使得∠EPF=90°,如图3,作∠PEG=∠BEP,求∠AEG与∠PFD度数的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设三角形三个内角的度数分别为x,y,z,如果其中一个角的度数是另一个角的度数的2倍,那么我们称数对(y,z)(y≤z)是x的和谐数对.例:当x=150°时,对应的和谐数对有一个,它为(10,20);当x=66时,对应的和谐数对有二个,它们为(33,81),(38,76).当对应的和谐数对(y,z)有三个时,此时x的取值范围是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,点A的坐标为(2x+y﹣3,x﹣2y),它关于x轴的对称点A1的坐标为(x+3,y﹣4),关于y轴的对称点为A2.
(1)求A1、A2的坐标;
(2)证明:O为线段A1A2的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( ) 
A.50°
B.60°
C.70°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=CB,BE=BF,点A,B,C在同一条直线上,∠1=∠2.
(1)证明:△ABE≌△CBF;
(2)若∠FBE=40°,∠C=45°,求∠E的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
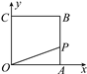
【题目】如图所示,已知正方形OABC,A(4,0),C(0,4),动点P从点A出发,沿ABCO的路线匀速运动,设动点P的运动路程为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )

A. (A) B. (B) C. (C) D. (D)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com