
【题目】如图△ABC为等边三角形,直线a∥AB,D为直线BC上一点,∠ADE交直线a于点E,且∠ADE=60°.
(1)若D在BC上(如图1)求证CD+CE=CA;

(2)若D在CB延长线上,CD、CE、CA存在怎样数量关系,给出你的结论并证明.
【答案】(1)证明见解析;(2)CD、CE、CA满足CE+CA=CD,证明见解析.
【解析】
(1)实际上也就是求两条线段相等,在AC上取一点F,使CF=CD,然后求证△ADF≌△EDC即可;(2)归根究底仍是求两条线段的问题,通过求证全等,最终得出几条边之间的关系.
(1)证明:在AC上取点F,使CF=CD,连接DF.
∵∠ACB=60°,
∴△DCF为等边三角形.
∴∠3+∠4=∠4+∠5=60°.
∴∠3=∠5.
∵∠1+∠ADE=∠2+∠ACE,
∴∠1=∠2.
在△ADF和△EDC中,
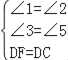 ,
,
∴△ADF≌△EDC(AAS).
∴CE=AF.
∴CD+CE=CF+AF=CA.
(2)解:CD、CE、CA满足CE+CA=CD;
证明:
在CA延长线上取CF=CD,连接DF.
∵△ABC为等边三角形,
∴∠ACD=60°,
∵CF=CD,
∴△FCD为等边三角形.
∵∠1+∠2=60°,
∵∠ADE=∠2+∠3=60°,
∴∠1=∠3.
在△DFA和△DCE中
 ,
,
∴△DFA≌△DCE(ASA).
∴AF=CE.
∴CE+CA=FA+CA=CF=CD.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图数轴上A、B、C三点对应的数分别是a、b、7,满足OA=3,BC=1,P为数轴上一动点,点P从A出发,沿数轴正方向以每秒1.5个单位长度的速度匀速运动,点Q从点C出发在射线CA上向点A匀速运动,且P、Q两点同时出发.
(1)求a、b的值
(2)当P运动到线段OB的中点时,点Q运动的位置恰好是线段AB靠近点B的三等分点,求点Q的运动速度
(3)当P、Q两点间的距离是6个单位长度时,求OP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB∥CD,点P为定点,E、F分别是AB、CD上的动点.
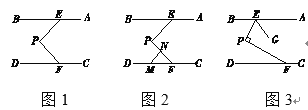
(1)求证:∠P=∠BEP+∠PFD;
(2)若点M为CD上一点,如图2,∠FMN=∠BEP,且MN交PF于N.试说明∠EPF与∠PNM的数量关系,并证明你的结论;
(3)移动E、F使得∠EPF=90°,如图3,作∠PEG=∠BEP,求∠AEG与∠PFD度数的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,点A的坐标为(2x+y﹣3,x﹣2y),它关于x轴的对称点A1的坐标为(x+3,y﹣4),关于y轴的对称点为A2.
(1)求A1、A2的坐标;
(2)证明:O为线段A1A2的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( ) 
A.50°
B.60°
C.70°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 |
|
|
5≤x<6 | 10 | 20% |
6≤x<7 |
| 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |

(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=CB,BE=BF,点A,B,C在同一条直线上,∠1=∠2.
(1)证明:△ABE≌△CBF;
(2)若∠FBE=40°,∠C=45°,求∠E的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
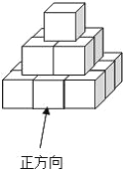
【题目】把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有 小正方体?
(2)其中两面被涂到的有 个小正方体;没被涂到的有 个小正方体;
(3)求出涂上颜色部分的总面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料.
我们知道,1+2+3+…+n=![]() ,那么12+22+32+…+n2结果等于多少呢?
,那么12+22+32+…+n2结果等于多少呢?
在图1所示三角形数阵中,第1行圆圈中的数为1,即12,第2行两个圆圈中数的和为2+2,即22,…;第n行n个圆圈中数的和为n+n+n+…+n,即n2.这样,该三角形数阵中共有![]() 个圆圈,所有圆圈中数的和为12+22+32+…+n2.
个圆圈,所有圆圈中数的和为12+22+32+…+n2.

(规律探究)
将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n﹣1行的第一个圆圈中的数分别为n﹣1,2,n),发现每个位置上三个圆圈中数的和均为 ,由此可得,这三个三角形数阵所有圆圈中数的总和为3(12+22+32+…+n2)= ,因此,12+22+32+…+n2= .
(解决问题)
根据以上发现,计算:![]() 的结果为 .
的结果为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com