
����Ŀ���Ķ����ϣ�
����֪����1+2+3+��+n=![]() ����ô12+22+32+��+n2������ڶ����أ�
����ô12+22+32+��+n2������ڶ����أ�
��ͼ1��ʾ�����������У���1��ԲȦ�е���Ϊ1����12����2������ԲȦ�����ĺ�Ϊ2+2����22��������n��n��ԲȦ�����ĺ�Ϊn+n+n+��+n����n2���������������������й���![]() ��ԲȦ������ԲȦ�����ĺ�Ϊ12+22+32+��+n2��
��ԲȦ������ԲȦ�����ĺ�Ϊ12+22+32+��+n2��

������̽����
������������������ת�ɵ���ͼ2��ʾ�����������۲��������������������ͬһλ��ԲȦ�е��������n��1�еĵ�һ��ԲȦ�е����ֱ�Ϊn��1��2��n��������ÿ��λ��������ԲȦ�����ĺ;�Ϊ�� �����ɴ˿ɵã���������������������ԲȦ�������ܺ�Ϊ3��12+22+32+��+n2��=�� ������ˣ�12+22+32+��+n2=�� ����
��������⣩
�������Ϸ��֣����㣺![]() �Ľ��Ϊ�� ����
�Ľ��Ϊ�� ����
���𰸡�2n+1��![]() ��
��![]() ��7.
��7.
��������
����ͼ1��ͼ2�������ܽ�õ�һ���Թ��ɣ����ô˹���ȷ�������ɣ�
�⣺������̽����
������������������ת�ɵ���ͼ2��ʾ�����������۲��������������������ͬһλ��ԲȦ�е��������n��1�еĵ�һ��ԲȦ�е����ֱ�Ϊn��1��2��n��������ÿ��λ��������ԲȦ�����ĺ;�2n+1���ɴ˿ɵã���������������������ԲȦ�������ܺ�Ϊ3��12+22+32+��+n2��=![]() ����ˣ�12+22+32+��+n2=
����ˣ�12+22+32+��+n2=![]() ��
��
��������⡿
�������Ϸ��֣����㣺��![]() �Ľ��Ϊ7��
�Ľ��Ϊ7��
�ʴ�Ϊ��2n+1��![]() ��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCΪ�ȱ������Σ�ֱ��a��AB��DΪֱ��BC��һ�㣬��ADE��ֱ��a�ڵ�E���ҡ�ADE=60�㣮
��1����D��BC�ϣ���ͼ1����֤CD+CE=CA��

��2����D��CB�ӳ����ϣ�CD��CE��CA��������������ϵ��������Ľ��۲�֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ABC=50�㣬��ACB=60�㣬��E��BC���ӳ����ϣ���ABC��ƽ����BD���ACE��ƽ����CD�ཻ�ڵ�D������AD�����н����в���ȷ���ǣ� ��

A. ��BAC=70�� B. ��DOC=90�� C. ��BDC=35�� D. ��DAC=55��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
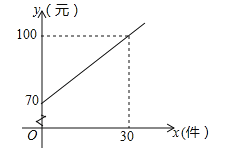
����Ŀ��ij��ݹ�˾��ÿλ�����С�硱��������ÿ�յ���������һ�κ�����ϵ����ͼ��ʾ��
��1����ÿλ�����С�硱��������y��Ԫ������������x������֮��ĺ�����ϵʽ��
��2����֪ij�����С�硱�������벻����110Ԫ����������Ҫ���Ͷ��ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=x2+bx+c��y=x��ͼ����ͼ��ʾ�������½��ۣ���b2��4c��0����b+c+1=0����3b+c+6=0���ܵ�1��x��3ʱ��x2+��b��1��x+c��0��������ȷ�ĸ��������� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�����е�B��x����������ϣ���C��y����������ϣ��߶�OB��OC�ij���OB��OC���Ƿ���x2��10x+16=0�����������������ߵĶԳ�����ֱ��x=��2��
��1����A��B��C��������ꣻ
��2����������ߵı���ʽ��
��3������AC��BC������E���߶�AB�ϵ�һ�����㣨���A����B���غϣ�������E��EF��AC��BC�ڵ�F������CE����AE�ij�Ϊm����CEF�����ΪS����S��m֮��ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
��4���ڣ�3���Ļ�������˵��S�Ƿ�������ֵ�������ڣ������S�����ֵ���������ʱ��E�����꣬�жϴ�ʱ��BCE����״���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��0��0����A��2��0��Ϊ����������OAP1 �� �Ե�P1���߶�P1A���е�BΪ����������P1BP2 �� ���Ե�P2���߶�P2B���е�CΪ��������P2CP3 �� ������˼�����ȥ������������������У����ڵ�������������ϵĶ���P6�������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪BDƽ�֡�ABF���ҽ�AE�ڵ�D��
��1����������BAE��ƽ����AP��Ҫ�߹���ͼ��������ͼ�ۼ�����д��������
��2����AP��BD�ڵ�O����BF�ڵ�C������CD����AC��BDʱ����֤���ı���ABCD�����Σ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com