
【题目】已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2﹣10x+16=0的两个根,且抛物线的对称轴是直线x=﹣2.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值?若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
【答案】
(1)
解:解方程x2﹣10x+16=0得x1=2,x2=8
∵点B在x轴的正半轴上,点C在y轴的正半轴上,且OB<OC
∴点B的坐标为(2,0),点C的坐标为(0,8)
又∵抛物线y=ax2+bx+c的对称轴是直线x=﹣2
∴由抛物线的对称性可得点A的坐标为(﹣6,0)
(2)
解:∵点C(0,8)在抛物线y=ax2+bx+c的图象上
∴c=8,将A(﹣6,0)、B(2,0)代入表达式,
得: ![]()
解得 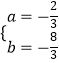
∴所求抛物线的表达式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+8
x+8
(3)
解:依题意,AE=m,则BE=8﹣m,
∵OA=6,OC=8,
∴AC=10
∵EF∥AC
∴△BEF∽△BAC
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]()
∴EF= ![]()
过点F作FG⊥AB,垂足为G,
则sin∠FEG=sin∠CAB= ![]()
∴ ![]() =
= ![]()
∴FG= ![]()
![]() =8﹣m
=8﹣m
∴S=S△BCE﹣S△BFE
= ![]() (8﹣m)×8﹣
(8﹣m)×8﹣ ![]() (8﹣m)(8﹣m)
(8﹣m)(8﹣m)
= ![]() (8﹣m)(8﹣8+m)
(8﹣m)(8﹣8+m)
= ![]() (8﹣m)m
(8﹣m)m
=﹣ ![]() m2+4m
m2+4m
自变量m的取值范围是0<m<8
(4)
解:存在.
理由:∵S=﹣ ![]() m2+4m=﹣
m2+4m=﹣ ![]() (m﹣4)2+8且﹣
(m﹣4)2+8且﹣ ![]() <0,
<0,
∴当m=4时,S有最大值,S最大值=8
∵m=4,
∴点E的坐标为(﹣2,0)
∴△BCE为等腰三角形.

【解析】(1)先解一元二次方程,得到线段OB、OC的长,也就得到了点B、C两点坐标,根据抛物线的对称性可得点A坐标;(2)把A、B、C三点代入二次函数解析式就能求得二次函数解析式;(3)易得S△EFF=S△BCE﹣S△BFE , 只需利用平行得到三角形相似,求得EF长,进而利用相等角的正弦值求得△BEF中BE边上的高;(4)利用二次函数求出最值,进而求得点E坐标.OC垂直平分BE,那么EC=BC,所求的三角形是等腰三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB=CB,BE=BF,点A,B,C在同一条直线上,∠1=∠2.
(1)证明:△ABE≌△CBF;
(2)若∠FBE=40°,∠C=45°,求∠E的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知正方形OABC,A(4,0),C(0,4),动点P从点A出发,沿ABCO的路线匀速运动,设动点P的运动路程为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
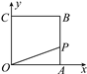

A. (A) B. (B) C. (C) D. (D)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料.
我们知道,1+2+3+…+n=![]() ,那么12+22+32+…+n2结果等于多少呢?
,那么12+22+32+…+n2结果等于多少呢?
在图1所示三角形数阵中,第1行圆圈中的数为1,即12,第2行两个圆圈中数的和为2+2,即22,…;第n行n个圆圈中数的和为n+n+n+…+n,即n2.这样,该三角形数阵中共有![]() 个圆圈,所有圆圈中数的和为12+22+32+…+n2.
个圆圈,所有圆圈中数的和为12+22+32+…+n2.

(规律探究)
将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n﹣1行的第一个圆圈中的数分别为n﹣1,2,n),发现每个位置上三个圆圈中数的和均为 ,由此可得,这三个三角形数阵所有圆圈中数的总和为3(12+22+32+…+n2)= ,因此,12+22+32+…+n2= .
(解决问题)
根据以上发现,计算:![]() 的结果为 .
的结果为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,都是由边长为 1 的正方体叠成的立体图形,例如第⑴个图形由 1 个正方体叠成,第⑵个图形由 4 个正方体叠成,第⑶个图形由 10 个正方体叠成,依次规律,第⑺个图形由( )个正方形叠成.

A. 86 B. 87 C. 85 D. 84
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级⑴班想买一些运动器材供班上同学阳光体育活动使用,班主任安排班长去商店买篮球和排球,下面是班长与售货员的对话:
班长:阿姨,您好! 售货员:同学,你好,想买点什么?
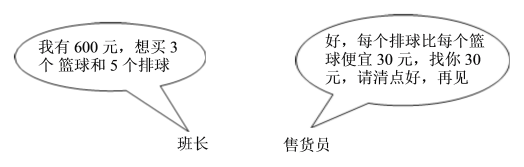
⑴根据这段对话,你能算出篮球和排球的单价各是多少吗?
⑵六一儿童节店里搞活动有两种套餐,1、套装打折:五个篮球和五个排球为一套装,套装打 八折:2、满减活动:999 减 100,1999 减 200;两种活动不重复参与,学校需要 15个篮球,13 个排球作为奖品,请问如何安排购买更划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知∠AOB和一条定长线段a,在∠AOB内找一点P,使点P到OA,OB的距离都等于a,作法如下:
①在∠AOB内作OB的垂线段NH,使NH=a,H为垂足;②过N作NM∥OB;③作∠AOB的平分线OP,与NM交于点P;④点P即为所求.其中③的依据是( )

A. 平行线之间的距离处处相等 B. 角的内部到角的两边的距离相等的点在角的平分线上
C. 角的平分线上的点到角的两边的距离相等 D. 线段垂直平分线上的点到线段两端点的距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E点,DF⊥AC于F点,有下列结论:①BD=DC;②DE=DF;③AD上任意一点到AB,AC的距离相等;④AD上任意一点到B点与C点的距离不等.其中正确的是( )

A. ①② B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,再解决问题,例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0
∴n=3,m=﹣3
(1)若x2+2y2﹣2xy+4y+4=0,求xy的值
(2)已知△ABC的三边长a,b,c都是正整数,且满足a2+b2﹣6a﹣6b+18+|3﹣c|=0,请问△ABC是怎样形状的三角形?
(3)根据以上的方法是说明代数式:x2+4x+y2﹣8y+21的值一定是一个正数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com