
����Ŀ�����꼶��������һЩ�˶����Ĺ�����ͬѧ���������ʹ���������ΰ��Űȥ�̵�������������������ǰ���ۻ�Ա�ĶԻ���
������������ã� �ۻ�Ա��ͬѧ������������ʲô��
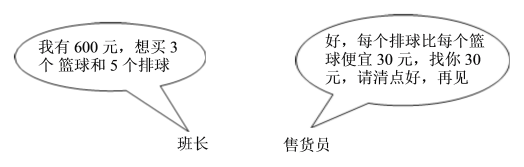
��������ζԻ�������������������ĵ��۸��Ƕ�������
����һ��ͯ�ڵ�����������ײ���1����װ���ۣ����������������Ϊһ��װ����װ�� ������2���������999 �� 100��1999 �� 200�����ֻ���ظ�������ѧУ��Ҫ 15������13 ��������Ϊ��Ʒ��������ΰ��Ź�������㣿
���𰸡���1������ĵ���Ϊ 90 Ԫ/��������ĵ���Ϊ 60 Ԫ/������2������װ���۹�������㣮
��������
��1��������ĵ���ΪxԪ/��������ĵ���ΪyԪ/��������ÿ�������ÿ���������30Ԫ��570Ԫ����3�������5�����������ɵó�����x��y�Ķ�Ԫһ�η���������֮���ɵó�������
��2���ֱ��������װ���۹����������������������ȽϺɵó�������
��1��������ĵ���ΪxԪ/��������ĵ���ΪyԪ/���������������
![]()
�����![]() ��
��
��������ĵ���Ϊ90Ԫ/��������ĵ���Ϊ60Ԫ/����
��2������װ���۹����踶����Ϊ��10����90+60����0.8+5��90+3��60=1830��Ԫ����������������踶����Ϊ��15��90+13��60��200=1930��Ԫ����
��1830��1930���ఴ��װ���۹����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A=3a2b��2ab2+abc��С��ͬѧ������2A��B�����ɡ�2A+B������ý��Ϊ4a2b��3ab2+4abc��
(1)����B�ı���ʽ��
(2)���2A��B�Ľ����
(3)Сǿͬѧ˵(2)�еĽ���Ĵ�С��c��ȡֵ�أ�������a=![]() ��b=
��b=![]() ��
��
��(2)��ʽ�ӵ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
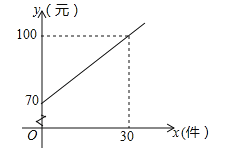
����Ŀ��ij��ݹ�˾��ÿλ�����С�硱��������ÿ�յ���������һ�κ�����ϵ����ͼ��ʾ��
��1����ÿλ�����С�硱��������y��Ԫ������������x������֮��ĺ�����ϵʽ��
��2����֪ij�����С�硱�������벻����110Ԫ����������Ҫ���Ͷ��ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�����е�B��x����������ϣ���C��y����������ϣ��߶�OB��OC�ij���OB��OC���Ƿ���x2��10x+16=0�����������������ߵĶԳ�����ֱ��x=��2��
��1����A��B��C��������ꣻ
��2����������ߵı���ʽ��
��3������AC��BC������E���߶�AB�ϵ�һ�����㣨���A����B���غϣ�������E��EF��AC��BC�ڵ�F������CE����AE�ij�Ϊm����CEF�����ΪS����S��m֮��ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
��4���ڣ�3���Ļ�������˵��S�Ƿ�������ֵ�������ڣ������S�����ֵ���������ʱ��E�����꣬�жϴ�ʱ��BCE����״���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ������ABC�У���ABC����ACB��ƽ�����ཻ��F����F��DE��BC���ֱ�AB��AC�ڵ�D��E���ж�DE=DB+EC�Ƿ������Ϊʲô��
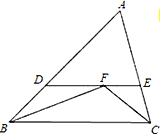
��2����ͼ������F����ABC��ƽ���ߺ������ACG��ƽ���ߵĽ��㣬�����������䣬������߶�DE��DB��EC֮���к�������ϵ��
֤����IJ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��0��0����A��2��0��Ϊ����������OAP1 �� �Ե�P1���߶�P1A���е�BΪ����������P1BP2 �� ���Ե�P2���߶�P2B���е�CΪ��������P2CP3 �� ������˼�����ȥ������������������У����ڵ�������������ϵĶ���P6�������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������У��� A ��ʾ 1���� B ��ʾ��2���ش���������⣺
(1)A��B ֮��ľ����� ��
(2)�۲����ᣬ��� A �ľ���Ϊ 5 �ĵ��ʾ�����ǣ� ��
(3)���������۵���ʹ�� A �룭3 ��ʾ�ĵ��غϣ���� B ���� ��ʾ�ĵ��غϣ�
(4)�������� M��N ����֮��ľ���Ϊ 2018��M �� N ����ࣩ���� M��N ���㾭��(3)���� �� �� �� �� �� �� �� �� M �� N �� �� �� ʾ �� �� �� �� �� �� M �� ��N�� ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ԭ���������y=��x2+2mx��m��0����x�����һ������ΪA������P��1��m����ֱ��PM��x���ڵ�M�����������ڵ�B���ǵ�B���������߶Գ���ĶԳƵ�ΪC��B��C���غϣ�������CB��CP��
��1����m=3ʱ�����A�����꼰BC�ij���
��2����m��1ʱ������CA����mΪ��ֵʱCA��CP��
��3������P��PE��PC��PE=PC�����Ƿ����m��ʹ�õ�E�����������ϣ������ڣ������������Ҫ���m��ֵ�����������Ӧ�ĵ�E���ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com