
����Ŀ����ͼ��ʾ,��֪��AOB��һ�������߶�a,����AOB����һ��P,ʹ��P��OA,OB�ľ��붼����a,��������:
������AOB����OB�Ĵ��߶�NH,ʹNH=a,HΪ����;�ڹ�N��NM��OB;������AOB��ƽ����OP,��NM���ڵ�P;�ܵ�P��Ϊ����.���Т۵�������(����)

A. ƽ����֮��ľ��봦����� B. �ǵ��ڲ����ǵ����ߵľ�����ȵĵ��ڽǵ�ƽ������
C. �ǵ�ƽ�����ϵĵ㵽�ǵ����ߵľ������ D. �߶δ�ֱƽ�����ϵĵ㵽�߶����˵�ľ������

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ�ٰ���ӭ������֪ʶ��������һ���������Ƚ���12������Ʒ���ŷ������±���
һ�Ƚ� | ���Ƚ� | ���Ƚ� |
1�и���1ö���� | 1�и��� | 1ö���� |
���ڹ���Ʒ���ܷ��ò�����1000Ԫ��������1100Ԫ��С���ڹ���������������ǰ���˽������Ϣ��
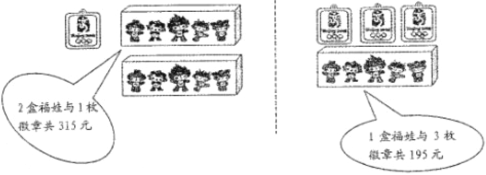
��1����һ������������һö���¸�����Ԫ��
��2�������λ��һ�Ƚ�2��������Ƚ������Ƚ�Ӧ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=x2+bx+c��y=x��ͼ����ͼ��ʾ�������½��ۣ���b2��4c��0����b+c+1=0����3b+c+6=0���ܵ�1��x��3ʱ��x2+��b��1��x+c��0��������ȷ�ĸ��������� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�����е�B��x����������ϣ���C��y����������ϣ��߶�OB��OC�ij���OB��OC���Ƿ���x2��10x+16=0�����������������ߵĶԳ�����ֱ��x=��2��
��1����A��B��C��������ꣻ
��2����������ߵı���ʽ��
��3������AC��BC������E���߶�AB�ϵ�һ�����㣨���A����B���غϣ�������E��EF��AC��BC�ڵ�F������CE����AE�ij�Ϊm����CEF�����ΪS����S��m֮��ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
��4���ڣ�3���Ļ�������˵��S�Ƿ�������ֵ�������ڣ������S�����ֵ���������ʱ��E�����꣬�жϴ�ʱ��BCE����״���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�D��E�ֱ���AC��AB�ϵĵ㣬BD��CE�ཻ�ڵ�O�����������ĸ�������
�١�EBO=��DCO���ڡ�BEO=��CDO����BE=CD����OB=OC��

��1�������ĸ������У������������������ж�AB=AC���������д�����е����Σ�
��2��ѡ��1��С���е�һ�����Σ�˵��AB=AC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��0��0����A��2��0��Ϊ����������OAP1 �� �Ե�P1���߶�P1A���е�BΪ����������P1BP2 �� ���Ե�P2���߶�P2B���е�CΪ��������P2CP3 �� ������˼�����ȥ������������������У����ڵ�������������ϵĶ���P6�������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������9�£����������г�һ��������ѧ��Ʒʱ���������������ɸ�ij��ʼDZ����ס��������ľߵ궼���㹻�����ĸÿ�ʼDZ����������ľߵ�ÿ�ʼDZ���۶���20Ԫ/�������ľߵ�����۷����ǣ�����ñʼDZ�������������5��ʱ��ԭ�����ۣ�����ñʼDZ�����5��ʱ���ӵ�6����ʼ����۵İ��۳��ۣ����ľߵ�����۷����ǣ����ܹ�����ٸ��ÿ�ʼDZ���һ�ɰ���۵ľ��۳��ۣ�
��1����������Ҫ����x��x��5�����ÿ�ʼDZ������ú�x�Ĵ���ʽ�ֱ��ʾ�����ľߵ�����ľߵ깺��ȫ���ÿ�ʼDZ�����ķ��ã�
��2���ڣ�1���������£���������ٸ��ʼDZ�ʱ�������ľߵ깺��ȫ���ʼDZ�����ķ����뵽���ľߵ깺��ȫ���ʼDZ�����ķ�����ͬ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������AM��BN���߶�CD�������˵�C��D�ֱ�������BN��AM�ϣ��ҡ�A����BCD��108�㣮E���߶�AD��һ�㣨�����A��D�غϣ�����BDƽ�֡�EBC��
��1�����ABC�Ķ�����
��2������ͼ���ҳ����ABC��ȵĽǣ���˵�����ɣ�
��3����ƽ���ƶ�CD����AD��CD�����ADB���AEB�Ķ���֮���Ƿ�����CDλ�õı仯�������仯�����仯���ҳ��仯���ɣ������䣬��������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪˫����y= ![]() ��k��0������ֱ��������OABб��OA���е�D������ֱ�DZ�AB�ཻ�ڵ�C������A������Ϊ����8��6�������AOC�����Ϊ ��
��k��0������ֱ��������OABб��OA���е�D������ֱ�DZ�AB�ཻ�ڵ�C������A������Ϊ����8��6�������AOC�����Ϊ �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com