
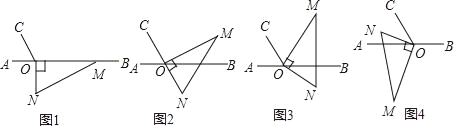
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角尺绕点O逆时针旋转至图2,使点N在OC的反向延长线上,请直接写出图中∠MOB的度数;
(2)将图1中的三角尺绕点O逆时针旋转至图3,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;
(3)将图1中的三角尺绕点O顺时针旋转至图4,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.
【答案】(1)30°;(2)150°;(3)∠AOM﹣∠NOC=30°,理由见解析
【解析】
(1) 根据对顶角求出∠BON,代入∠BOM=∠MON-∠BON求出即可;
(2) 求出么BOC=![]() , 根据角平分线定义请求出∠COM=∠BOM=
, 根据角平分线定义请求出∠COM=∠BOM=![]() , 代入∠CON=∠MON+∠COM求出即可;
, 代入∠CON=∠MON+∠COM求出即可;
(3)用∠AOM和∠CON表示出∠AON,然后列出方程整理即可得解.
(1)如图2,∵∠AOC=60°,
∴∠BON=∠AOC=60°,
∵∠MON=90°,
∴∠BOM=∠MON﹣∠BON=30°,
(2)∵∠AOC=60°,
∴∠BOC=180°﹣∠AOC=120°,
∵OM平分∠BOC,
∴∠COM=∠BOM=60°,
∵∠MON=90°,
∴∠CON=∠MON+∠COM=90°+60°=150°;
(3)∠AOM﹣∠NOC=30°,
理由是:∵∠MON=90°,∠AOC=60°,
∴∠AON=90°﹣∠AOM,
∠AON=60°﹣∠NOC,
∴90°﹣∠AOM=60°﹣∠NOC,
∴∠AOM﹣∠NOC=30°,
故∠AOM与∠NOC之间的数量关系为:∠AOM﹣∠NOC=30°.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】仅用无刻度的直尺,按要求画图(保留画图痕迹,不写作法)
(1)如图①,画出⊙O的一个内接矩形; 
(2)如图②,AB是⊙O的直径,CD是弦,且AB∥CD,画出⊙O的内接正方形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点D为边BC上一点,点E为边AB的中点,过点A作AF∥BC,交DE的延长线与点F,连接BF. 
(1)求证:四边形ADBF是平行四边形;
(2)若∠ADF=∠BDF,DF=2CD,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用边长为12cm的正方形硬纸板做三棱柱盒子,每个盒子的侧面为长方形,底面为等边三角形.
(1)每个盒子需 个长方形, 个等边三角形;
(2)硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面.

现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
① 用x的代数式分别表示裁剪出的侧面和底面的个数;
② 若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
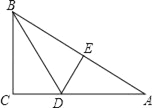
【题目】如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE.
(1)若∠A=25°,求∠BDC的度数.
(2)若AC=4,BC=2,求BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.
(1)请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠B=20°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M,N,再分别以点M,N为圆心,大于![]() MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC于点D,则∠ADB=________.
MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC于点D,则∠ADB=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,BC=AC,∠ACB=90°,D为射线AB上一点,连接CD,过点C作线段CD的垂线l,在直线l上,分别在点C的两侧截取与线段CD相等的线段CE和CF,连接AE,BF.
(1)当点D在线段AB上时(点D不与点A,B重合),如图23(a).
①请你将图形补充完整;
②线段BF,AD所在直线的位置关系为________,线段BF,AD的数量关系为________.
(2)当点D在线段AB的延长线上时,如图23(b).
在(1)中②问的结论是否仍然成立?如果成立,请进行证明;如果不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小琳、晓明两人在100m的跑道上匀速跑步训练,他们同时从起点出发,跑向终点.
(1)设小琳速度为v(m/s),写出小琳跑完全程所用的时间t(s)与速度v(m/s)之间的函数关系式;
(2)已知晓明的速度是小琳速度的1.25倍,两人跑完全程,小琳要比晓明多用4s,用分式方程求小琳、晓明两人匀速跑步的速度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com