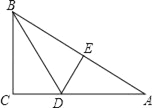
【题目】如图，在Rt△ABC中，∠C=90°，把AB对折后，点A与点B重合，折痕为DE．
（1）若∠A=25°，求∠BDC的度数．
（2）若AC=4，BC=2，求BD．
名师导航单元期末冲刺100分系列答案科目：初中数学 来源： 题型：
【题目】现有一“过关游戏”，规定：在第n关要掷一颗骰子n次，如果这n次抛掷所出现的点数之和大于 
，则算过关，否则不算过关．
（1）过第1关是事件（填“必然”、“不可能”或“不确定”，后同），过第4关是事件；
（2）当n=2时，计算过过第二关的概率（可借助表格或树状图）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图，已知点C在线段AB上，线段AC＝6，BC＝4，点M、N分别是AC、BC的中点，求MN的长度；
（2）根据（1）的计算过程与结果，设AC＋BC＝a，其它条件不变，请猜想出MN的长度吗？并说明理由；
（3）对于（1）题，如果将“点C在线段AB上”改为“点C在射线AB上”，其它条件不变，求MN的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪（裁剪后边角料不再利用）
A方法：剪6个侧面； B方法：剪4个侧面和5个底面。
现有19张硬纸板，裁剪时
张用A方法，其余用B方法。
（1）用的代数式分别表示裁剪出的侧面和底面的个数；
（2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？
查看答案和解析>>
科目：初中数学 来源： 题型：
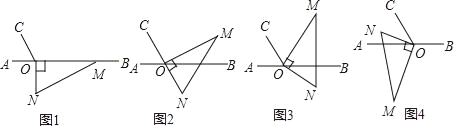
【题目】如图1，点O为直线AB上一点，过点O作射线OC，使∠AOC=60°，将一把直角三角尺的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．
（1）将图1中的三角尺绕点O逆时针旋转至图2，使点N在OC的反向延长线上，请直接写出图中∠MOB的度数；
（2）将图1中的三角尺绕点O逆时针旋转至图3，使一边OM在∠BOC的内部，且恰好平分∠BOC，求∠CON的度数；
（3）将图1中的三角尺绕点O顺时针旋转至图4，使ON在∠AOC的内部，请探究∠AOM与∠NOC之间的数量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算下列各题：
(1)（-0.5）+|0-6
|-（-7
）-（-4.75）
(2)-14-（1-0×4）÷
×[（-2）2-6]；
(3)（-1）2017+1-22+41-（-+
）×（-24）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】结合数轴与绝对值的知识回答下列问题：
数轴上表示4和1的两点之间的距离是3：而|4-1|=3；表示-3和2两点之间的距离是5：而|-3-2|=5；表示-4和-7两点之间的距离是3，而|-4-（-7）|=3．
一般地，数轴上表示数m和数n的两点之间的距离公式为|m-n|．
(1)数轴上表示数-5的点与表示-2的点之间的距离为______；
(2)数轴上表示数a的点与表示-4的点之间的距离表示为______；若数轴上a位于-4与2之间，求|a+4|+|a-2|的值；
(3)如果表示数a和3的两点之间的距离是7，则可记为：|a-3|=7，求a的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】列方程解应用题：
（1）一个箱子，如果装橙子可以装18个，如果装梨可以装16个，现共有橙子、梨400个，而且装梨的箱子是装橙子箱子的2倍．请算一下，装橙子和装梨的箱子各多少个？
（2）一群小孩分一堆苹果，每人3个多7个，每人4个少3个，求有几个小孩？几个苹果？
（3）一架飞机在两城之间飞行，风速为24千米/时．顺风飞行需要2小时50分，逆风飞行需要3小时，求无风时飞机的速度和两城之间的航程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
