
【题目】现有一“过关游戏”,规定:在第n关要掷一颗骰子n次,如果这n次抛掷所出现的点数之和大于 ![]() ,则算过关,否则不算过关.
,则算过关,否则不算过关.
(1)过第1关是事件(填“必然”、“不可能”或“不确定”,后同),过第4关是事件;
(2)当n=2时,计算过过第二关的概率(可借助表格或树状图).
【答案】
(1)必然;不可能
(2)解:n=2时,
画树状图为:
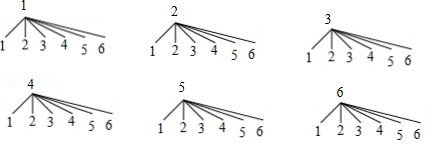
共有36种可等可能的结果数,其中这2次抛掷所出现的点数之和大于 ![]() 的结果数为33,
的结果数为33,
所以过第二关的概率= ![]() =
= ![]()
【解析】解:(1)第1次抛掷所出现的点数大于等于1,即大于 ![]() ,所以过第1关是必然事件,过第4关是不可能事件; 所以答案是必然,不可能;
,所以过第1关是必然事件,过第4关是不可能事件; 所以答案是必然,不可能;
【考点精析】关于本题考查的随机事件和列表法与树状图法,需要了解在条件S下,一定会发生的事件,叫相对于条件S的必然事件;在条件S下,一定不会发生的事件,叫相对于条件S的不可能事件;在条件S下可能发生也可能不发生的事件,叫相对于S的随机事件;当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】规定:求若干个相同的有理数(均不等于 0)的除法运算叫做除方,如 2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等,类比有理数的乘方,我们把记作 2÷2÷2,2②,读作“2的圈 3 次方,”(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作:“(﹣3)的圈 4 次方”.一般地,把![]() 个
个![]() 记作 a,读作 “a 的圈 n次方”
记作 a,读作 “a 的圈 n次方”
(初步探究)
(1)直接写出计算结果:2②,(﹣![]() )②.
)②.
(深入思考)
![]()
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
(2)试一试,仿照上面的算式,将下列运算结果直接写成幂的形式.
5⑥;(﹣![]() )⑩.
)⑩.
(3)想一想:有理数 a(a≠0)的圈n(n≥3)次方写成幂的形式等于多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由相同边长的小正方形组成的网格图形,A、B、C都在格点上,利用网格画图:(注:所画线条用黑色签字笔描黑)
(1)过点C画AB的平行线;
(2)过点B画AC的垂线,垂足为点G;过点B画AB的垂线,交AC的延长线于H.
(3)点B到AC的距离是线段 的长度,线段AB的长度是点 到直线
的距离.
(4)线段BG、AB的大小关系为:BG AB(填“>”、“<”或“=”),理由是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)比较大小;
①|﹣2|+|3| |﹣2+3|;
②|4|+|3| |4+3|;
③|﹣![]() |+|﹣
|+|﹣![]() | |﹣
| |﹣![]() +(﹣
+(﹣![]() )|;
)|;
④|﹣5|+|0| |﹣5+0|.
(2)通过(1)中的大小比较,猜想并归纳出|a|+|b|与|a+b|的大小关系,并说明a,b满足什么关系时,|a|+|b|=|a+b|成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细观察下面由“※”组成的图案和算式,解答问题:

1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)请计算:
1+3+5+7+9+ … +19= ;
(2)请猜想:
1+3+5+7+9+ … +(2n-1)+(2n+1)+(2n+3)= ;
(3)请用上述规律计算:
103+105+107+ … +2013+2015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仅用无刻度的直尺,按要求画图(保留画图痕迹,不写作法)
(1)如图①,画出⊙O的一个内接矩形; 
(2)如图②,AB是⊙O的直径,CD是弦,且AB∥CD,画出⊙O的内接正方形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,∠AOC=∠BOD=90°.
(1)如果∠DOC=28°,那么∠AOB 的度数是多少?
(2)∠AOD ∠BOC(填“>”、“=”或“<”),理由是 .
(3)在图2 中利用能够画直角的工具再画一个与∠COB 相等的角.

查看答案和解析>>
科目:初中数学 来源: 题型:
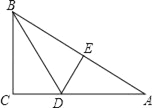
【题目】如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE.
(1)若∠A=25°,求∠BDC的度数.
(2)若AC=4,BC=2,求BD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com