
【题目】如图 1,∠AOC=∠BOD=90°.
(1)如果∠DOC=28°,那么∠AOB 的度数是多少?
(2)∠AOD ∠BOC(填“>”、“=”或“<”),理由是 .
(3)在图2 中利用能够画直角的工具再画一个与∠COB 相等的角.

【答案】(1)152°;(2)=,同角的余角相等;(3)详见解析.
【解析】
(1)根据∠AOC=90°,∠DOC=28°,求出∠AOD的度数,然后即可求出∠AOB的度数;
(2)根据同角的余角相等即可得出结论;
(3)首先以OB为边,在∠BOC外画∠BOD=90°,再以OC为边在∠COD外画∠AOC=90°,即可得到∠AOD=∠BOC.
(1)∵∠AOC=∠DOB=90°,∠DOC=28°,∴∠AOD=90°﹣28°=62°,∴∠AOB=90°+62°=152°.
(2)∠AOD=∠BOC,理由是:同角的余角相等(或见下面解释)
∵∠AOC=∠DOB=90°,∴∠AOD+∠DOC=∠BOC+∠DOC,∴∠AOD=∠BOC;
(3)如图所示:∠AOD=∠BOC.


科目:初中数学 来源: 题型:
【题目】如图,将平行四边形ABCD绕点A逆时针旋转40°,得到平行四边形AB′C′D′,若点B′恰好落在BC边上,则∠DC′B′的度数为( )
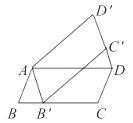
A. 60° B. 65° C. 70° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一“过关游戏”,规定:在第n关要掷一颗骰子n次,如果这n次抛掷所出现的点数之和大于 ![]() ,则算过关,否则不算过关.
,则算过关,否则不算过关.
(1)过第1关是事件(填“必然”、“不可能”或“不确定”,后同),过第4关是事件;
(2)当n=2时,计算过过第二关的概率(可借助表格或树状图).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学五次数学测验成绩如下表:
请你在表中的空白处填上适当的数,用学到的统计知识对两位同学的成绩(单位:分)进行分析,并写出一条合理化建议.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用钉子把木棒AB,BC和CD分别在端点B,C处连接起来,AB,CD可以转动,用橡皮筋把AD连接起来,设橡皮筋AD的长是x cm.
(1)若AB=5 cm,CD=3 cm,BC=11 cm,求x的最大值和最小值;
(2)在(1)的条件下要围成一个四边形,你能求出橡皮筋长x的取值范围吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ACB和△DCE均为等边三角形,若B,D,E在同一直线上,连接AE.
(1)请你在图中找出一个与△AEC全等的三角形:;
(2)∠AEB的度数为;CE,AE,BE的数量关系为 .
(3)如图2,△ACB是等腰直角三角形,∠AEB=90°,连接CE,过点C作CD⊥CE,交BE于点D,试探究CE,AE,BE的数量关系,并说明理由.
(4)如图3,在正方形ABCD中,CD=5 ![]() ,点P为正方形ABCD外一点,∠APC=90°,且AP=6,试求点P到CD的距离.
,点P为正方形ABCD外一点,∠APC=90°,且AP=6,试求点P到CD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知点C在线段AB上,线段AC=6,BC=4,点M、N分别是AC、BC的中点,求MN的长度;
(2)根据(1)的计算过程与结果,设AC+BC=a,其它条件不变,请猜想出MN的长度吗?并说明理由;
(3)对于(1)题,如果将“点C在线段AB上”改为“点C在射线AB上”,其它条件不变,求MN的长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)(-0.5)+|0-6![]() |-(-7
|-(-7![]() )-(-4.75)
)-(-4.75)
(2)-14-(1-0×4)÷![]() ×[(-2)2-6];
×[(-2)2-6];
(3)(-1)2017+1-22+41-(![]() -
-![]() +
+![]() )×(-24)
)×(-24)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com