
【题目】如图,将平行四边形ABCD绕点A逆时针旋转40°,得到平行四边形AB′C′D′,若点B′恰好落在BC边上,则∠DC′B′的度数为( )
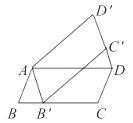
A. 60° B. 65° C. 70° D. 75°
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】如图①,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=40°,求∠DOE的度数;
(2)如图①,若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示)
(3)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,OE平分∠BOC.
①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
②在∠AOC的内部有一条射线OF,且∠AOC﹣3∠AOF=2∠BOE,试确定∠AOF与∠DOE的度数之间的关系,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了备战初三物理、化学实验操作考试,某校对初三学生进行了模拟训练,物理、化学各有4各不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示,测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.
(1)请用树形图法或列表法,表示某个同学抽签的各种可能情况.
(2)小张同学对物理的①、②和化学的b、c号实验准备得较好,他同时抽到两科都准备的较好的实验题目的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由相同边长的小正方形组成的网格图形,A、B、C都在格点上,利用网格画图:(注:所画线条用黑色签字笔描黑)
(1)过点C画AB的平行线;
(2)过点B画AC的垂线,垂足为点G;过点B画AB的垂线,交AC的延长线于H.
(3)点B到AC的距离是线段 的长度,线段AB的长度是点 到直线
的距离.
(4)线段BG、AB的大小关系为:BG AB(填“>”、“<”或“=”),理由是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,再解决问题,例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0
∴n=3,m=﹣3
(1)若x2+2y2﹣2xy+4y+4=0,求xy的值
(2)已知△ABC的三边长a,b,c都是正整数,且满足a2+b2﹣6a﹣6b+18+|3﹣c|=0,请问△ABC是怎样形状的三角形?
(3)根据以上的方法是说明代数式:x2+4x+y2﹣8y+21的值一定是一个正数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)比较大小;
①|﹣2|+|3| |﹣2+3|;
②|4|+|3| |4+3|;
③|﹣![]() |+|﹣
|+|﹣![]() | |﹣
| |﹣![]() +(﹣
+(﹣![]() )|;
)|;
④|﹣5|+|0| |﹣5+0|.
(2)通过(1)中的大小比较,猜想并归纳出|a|+|b|与|a+b|的大小关系,并说明a,b满足什么关系时,|a|+|b|=|a+b|成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细观察下面由“※”组成的图案和算式,解答问题:

1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)请计算:
1+3+5+7+9+ … +19= ;
(2)请猜想:
1+3+5+7+9+ … +(2n-1)+(2n+1)+(2n+3)= ;
(3)请用上述规律计算:
103+105+107+ … +2013+2015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,∠AOC=∠BOD=90°.
(1)如果∠DOC=28°,那么∠AOB 的度数是多少?
(2)∠AOD ∠BOC(填“>”、“=”或“<”),理由是 .
(3)在图2 中利用能够画直角的工具再画一个与∠COB 相等的角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是线段CB上的异于B、C的动点,AF⊥AE交线段CD的延长线于点F,EF与AD交于点M.
(1)求证:△ABE∽△ADF;
(2)若AE⊥BD,求BE长;
(3)若△AEM是以AE为腰的等腰三角形,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com