
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是线段CB上的异于B、C的动点,AF⊥AE交线段CD的延长线于点F,EF与AD交于点M.
(1)求证:△ABE∽△ADF;
(2)若AE⊥BD,求BE长;
(3)若△AEM是以AE为腰的等腰三角形,求BE的长.
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠C=∠ADC=∠ADF=90°,AD∥BC,
∵AF⊥AE,∴∠EAF=90°,
∴∠BAD=∠EAF,
∴∠BAE=∠DAF,
∵∠ABE=∠ADF=90°,
∴△ABE∽△ADF
(2)
解:∵AD∥BC,
∴∠AEB=∠DAE,
∵AE⊥BD,
∴∠BAE+∠ABD=90°,
∵∠BAE+∠AEB=90°,
∴∠ABD=∠AEB,
∴∠AEB=∠ABD,
又∵∠ABE=∠BAD=90°,
∴△ABE∽△DAB,
∴ ![]() ,即
,即 ![]() ,
,
解得:BE= ![]()
(3)
解:分两种情况:
①当AE=AM时,∠AEF=∠AME,
∵AF⊥AE,
∴∠EAF=90°,
∵AD∥BC,
∴∠AME=∠CEF,
∴∠AEF=∠CEF,
在△AEF和△CEF中, 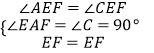 ,
,
∴△AEF≌△CEF(AAS),
∴AE=CE,
设BE=x,则AE=CE=4﹣x,Rt△ABE中,
由勾股定理得:x2+32=(4﹣x)2,解得:x= ![]() ;
;
②当AE=EM时,过点E作EN⊥AD于点N,如图所示:
则AN=MN=BE=x,EN∥DF,
由(1)得:△ABE∽△ADF,
∴ ![]() ,即
,即 ![]() ,
,
解得:DF= ![]() x,
x,
∵EN∥DF,
∴∴△EMN∽△FMD,
∴ ![]() ,即
,即 ![]() ,
,
解得:x= ![]() 或x=﹣6(舍去),
或x=﹣6(舍去),
∴BE= ![]() ;
;
综上所述,若△AEM是以AE为腰的等腰三角形,BE长为 ![]() 或
或 ![]() .
.
【解析】(1)由矩形的性质得出∠BAD=∠ABC=∠C=∠ADC=∠ADF=90°,AD∥BC,证出∠BAE=∠DAF,即可得出结论;(2)证明△ABE∽△DAB,得出对应边成比例,即可得出答案;(3)①当AE=AM时,证明△AEF≌△CEF(AAS),得出AE=CE,设BE=x,则AE=CE=4﹣x,Rt△ABE中,由勾股定理得出方程,解方程即可;②当AE=EM时,过点E作EN⊥AD于点N,则AN=MN=BE=x,EN∥DF,由(1)得:△ABE∽△ADF,得出对应边成比例求出DF= ![]() x,由平行线证明△EMN∽△FMD,得出对应边成比例,得出方程,解方程即可.
x,由平行线证明△EMN∽△FMD,得出对应边成比例,得出方程,解方程即可.
【考点精析】认真审题,首先需要了解相似三角形的应用(测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解).


科目:初中数学 来源: 题型:
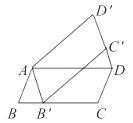
【题目】如图,将平行四边形ABCD绕点A逆时针旋转40°,得到平行四边形AB′C′D′,若点B′恰好落在BC边上,则∠DC′B′的度数为( )
A. 60° B. 65° C. 70° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ACB和△DCE均为等边三角形,若B,D,E在同一直线上,连接AE.
(1)请你在图中找出一个与△AEC全等的三角形:;
(2)∠AEB的度数为;CE,AE,BE的数量关系为 .
(3)如图2,△ACB是等腰直角三角形,∠AEB=90°,连接CE,过点C作CD⊥CE,交BE于点D,试探究CE,AE,BE的数量关系,并说明理由.
(4)如图3,在正方形ABCD中,CD=5 ![]() ,点P为正方形ABCD外一点,∠APC=90°,且AP=6,试求点P到CD的距离.
,点P为正方形ABCD外一点,∠APC=90°,且AP=6,试求点P到CD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知点C在线段AB上,线段AC=6,BC=4,点M、N分别是AC、BC的中点,求MN的长度;
(2)根据(1)的计算过程与结果,设AC+BC=a,其它条件不变,请猜想出MN的长度吗?并说明理由;
(3)对于(1)题,如果将“点C在线段AB上”改为“点C在射线AB上”,其它条件不变,求MN的长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形的边长为4,甲、乙两动点分别从正方形![]() 的顶点
的顶点![]() 同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若乙的速度是甲的速度的3倍,则它们第2 019次相遇在( )
同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若乙的速度是甲的速度的3倍,则它们第2 019次相遇在( )

A. ![]() 边上 B.
边上 B. ![]() 边上 C.
边上 C. ![]() 边上 D.
边上 D. ![]() 边上
边上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)(-0.5)+|0-6![]() |-(-7
|-(-7![]() )-(-4.75)
)-(-4.75)
(2)-14-(1-0×4)÷![]() ×[(-2)2-6];
×[(-2)2-6];
(3)(-1)2017+1-22+41-(![]() -
-![]() +
+![]() )×(-24)
)×(-24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com