
【题目】如图①,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=40°,求∠DOE的度数;
(2)如图①,若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示)
(3)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,OE平分∠BOC.
①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
②在∠AOC的内部有一条射线OF,且∠AOC﹣3∠AOF=2∠BOE,试确定∠AOF与∠DOE的度数之间的关系,说明理由.

【答案】(1)20°;(2)∠DOE=![]() ;(3)①∠DOE=
;(3)①∠DOE=![]() ∠AOC,理由见解析;②4∠EOD﹣3∠AOF=180°,理由见解析.
∠AOC,理由见解析;②4∠EOD﹣3∠AOF=180°,理由见解析.
【解析】
首先求得∠COB的度数,然后根据角平分线的定义求得∠COE的度数,再根据∠DOE=∠COD-∠COE即可求解;
解法与(1)相同,把①中的60°改成α即可;
①把∠AOC的度数作为已知量,求得∠BOC的度数,然后根据角的平分线的定义求得∠COE的度数,再根据∠DOE=∠COD-∠COE求得∠DOE,即可解决;
②由∠AOC﹣3∠AOF=2∠BOE, OE平分∠BOC,∠AOC和∠DOE的关系,可以建立各个角之间的关系,从而可以得到∠AOF与∠DOE的度数之间的关系.
(1)∵∠AOC=40°
∴∠COB=180°﹣∠AOC=180°﹣40°=140°
∵OE平分∠COB
∴∠COE=![]() ∠COB=70°,
∠COB=70°,
又∵∠COD=90°
∴∠EOD=∠COD﹣∠COE=20°
(2)∠DOE=![]() ,
,
(3)①∠DOE=![]() ∠AOC,理由如下:
∠AOC,理由如下:
∵OE平分∠COB
∴∠COE=![]() ∠COB
∠COB
又∵∠COD=90°
∴∠EOD=∠COD﹣∠COE=90°﹣![]() ∠COB,
∠COB,
∵∠COB+∠AOC=180°
∴∠COB=180°﹣∠AOC
∴∠EOD=90°﹣![]() (180°﹣∠AOC)=
(180°﹣∠AOC)=![]() ∠AOC
∠AOC
②4∠EOD﹣3∠AOF=180°,理由如下:
∵OE平分∠COB
∴∠EOB=∠COE
∴∠AOC﹣2∠BOE=∠AOC﹣2∠COE
=∠AOC﹣2(90°﹣∠EOD)
=∠AOC+2∠EOD﹣180°
又∵∠DOE=![]() ∠AOC
∠AOC
∴∠AOC﹣2∠BOE=4∠EOD﹣180°
∵∠AOC﹣3∠AOF=2∠BOE
∴4∠EOD﹣3∠AOF=180°


科目:初中数学 来源: 题型:
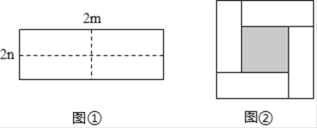
【题目】图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形.
(1)用两种不同的方法表示图②中小正方形(阴影部分)的面积:
方法一:S小正方形= ;
方法二:S小正方形= ;
(2)(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系为
(3)应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求x﹣y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,转盘上1、2、3、4四个数字分别代表鸡、猴、鼠、羊四种生肖邮票(每种邮票各两枚,鸡年邮票面值“80分”,其它邮票都是面值“1.20元”),转动转盘后,指针每落在某个数字所在扇形一次就表示获得该种邮票一枚. 
(1)任意转动转盘一次,获得猴年邮票的概率是;
(2)任意转动转盘两次,求获得的两枚邮票可以邮寄一封需2.4元邮资的信件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张在自家土地上平整出了一块苗圃,并将这块苗圃分成了四个长方形区域,其尺寸如图所示(图中长度单位:米),小张计划在这四个区域上按图中所示分别种植草本花卉 1 号、2 号、3 号、4 号.
(1)用式子表示这块苗圃的总面积;
(2)已知种植草本花卉 1 号、2 号、3 号、4 号的成本分别是每平方米 4 元、6 元、8 元、10 元.
①用式子表示小张在这块苗圃上种植草本花卉的总成本;
②当 a=9 时,求小张在这块苗圃上种植草本花卉的总成本.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有5张背面完全相同的卡片,正面分别写有 ![]() ,(
,( ![]() )0 ,
)0 , ![]() ,π,2﹣2 . 把卡片背面朝上洗匀后,从中随机抽取1张,其正面的数字是无理数的概率是 .
,π,2﹣2 . 把卡片背面朝上洗匀后,从中随机抽取1张,其正面的数字是无理数的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线EF与MN相交于点O,∠MOE=30°,将一直角三角尺的直角顶点与点O重合,直角边OA与MN重合,OB在∠NOE内部.操作:将三角尺绕点O以每秒5°的速度沿顺时针方向旋转一周,设运动时间为t(s).
(1)当t为何值时,直角边OB恰好平分∠NOE?此时OA是否平分∠MOE?请说明理由;
(2)若在三角尺转动的同时,直线EF也绕点O以每秒8°的速度顺时针方向旋转一周,当一方先完成旋转一周时,另一方同时停止转动.
①当t为何值时,OE平分∠AOB?
②OE能否平分∠NOB?若能请直接写出t的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张写着以下数字的卡片,请按要求抽出卡片,完成下列各题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字之积最大,最大值是________.
(2)从中取出2张卡片,使这2张卡片上数字之差最小,最小值是________.
(3)从中取出4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,请写出一种符合要求的运算式子________.(注:4个数字都必须用到且只能用一次.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将平行四边形ABCD绕点A逆时针旋转40°,得到平行四边形AB′C′D′,若点B′恰好落在BC边上,则∠DC′B′的度数为( )
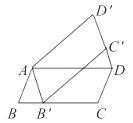
A. 60° B. 65° C. 70° D. 75°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com