
【题目】如图,用钉子把木棒AB,BC和CD分别在端点B,C处连接起来,AB,CD可以转动,用橡皮筋把AD连接起来,设橡皮筋AD的长是x cm.
(1)若AB=5 cm,CD=3 cm,BC=11 cm,求x的最大值和最小值;
(2)在(1)的条件下要围成一个四边形,你能求出橡皮筋长x的取值范围吗?

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在CD,BC上,且AF=BE,BE与AF相交于点G,则下列结论中错误的是( )
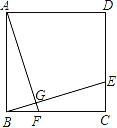
A. BF=CE B. ∠DAF=∠BEC
C. AF⊥BE D. ∠AFB+∠BEC=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)比较大小;
①|﹣2|+|3| |﹣2+3|;
②|4|+|3| |4+3|;
③|﹣![]() |+|﹣
|+|﹣![]() | |﹣
| |﹣![]() +(﹣
+(﹣![]() )|;
)|;
④|﹣5|+|0| |﹣5+0|.
(2)通过(1)中的大小比较,猜想并归纳出|a|+|b|与|a+b|的大小关系,并说明a,b满足什么关系时,|a|+|b|=|a+b|成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仅用无刻度的直尺,按要求画图(保留画图痕迹,不写作法)
(1)如图①,画出⊙O的一个内接矩形; 
(2)如图②,AB是⊙O的直径,CD是弦,且AB∥CD,画出⊙O的内接正方形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,∠AOC=∠BOD=90°.
(1)如果∠DOC=28°,那么∠AOB 的度数是多少?
(2)∠AOD ∠BOC(填“>”、“=”或“<”),理由是 .
(3)在图2 中利用能够画直角的工具再画一个与∠COB 相等的角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校有一个长方形广场,在广场的中央设计一个圆形花坛,四角都设计四分之一圆形的花坛.若长方形的长为am,宽为bm,中央圆形的半径和四个四分之一圆形的半径都为rm.
(1)列式表示广场空地的面积;(不写过程,直接写出答案)
(2)学校准备在广场四周种树,七年级四个班的学生在植树节当天进行义务植树,一班植树 x棵,二班植树的棵数比一班的多10棵,三班植树的棵数比二班的2倍少30棵,四班植树的棵数比三班的一半多20棵,求四个班一共植树多少棵?(用含x的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点D为边BC上一点,点E为边AB的中点,过点A作AF∥BC,交DE的延长线与点F,连接BF. 
(1)求证:四边形ADBF是平行四边形;
(2)若∠ADF=∠BDF,DF=2CD,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠B=20°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M,N,再分别以点M,N为圆心,大于![]() MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC于点D,则∠ADB=________.
MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC于点D,则∠ADB=________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com