
【题目】如图,在△ABC中,∠C=90°,点D为边BC上一点,点E为边AB的中点,过点A作AF∥BC,交DE的延长线与点F,连接BF. 
(1)求证:四边形ADBF是平行四边形;
(2)若∠ADF=∠BDF,DF=2CD,求∠ABC的度数.
【答案】
(1)证明:∵AF∥BC,
∴∠AFE=∠BDE,
在△AEF与△BED中, 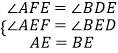 ,
,
∴△AEF≌△BED,
∴AF=BD,
∵AF∥BD,
∴四边形ADBF是平行四边形
(2)解:∵∠ADF=∠BDF,
∴∠ADF=∠AFD,
∴AD=AF,
∴ADBF是菱形,
∴DF=2DE,AE⊥DF,
∵DF=2CD,
∵∠C=90°,
∴DC=DE,
在Rt△ACD与Rt△AED中, ![]() ,
,
∴Rt△ACD≌Rt△AED,
∴AC=AE= ![]() AB,
AB,
∴∠ABC=30°
【解析】(1)根据平行线的性质得到∠AFE=∠BDE,根据全等三角形的性质得到AF=BD,于是得到结论;(2)根据已知条件得到ADBF是菱形,根据菱形的性质得到AB⊥DF,根据全等三角形的性质得到AC=AE= ![]() AB,于是得到结论.
AB,于是得到结论.
【考点精析】本题主要考查了直角三角形斜边上的中线和平行四边形的判定与性质的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,用钉子把木棒AB,BC和CD分别在端点B,C处连接起来,AB,CD可以转动,用橡皮筋把AD连接起来,设橡皮筋AD的长是x cm.
(1)若AB=5 cm,CD=3 cm,BC=11 cm,求x的最大值和最小值;
(2)在(1)的条件下要围成一个四边形,你能求出橡皮筋长x的取值范围吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°
(1)用尺规作AB的垂直平分线MN交BC于点P(不写作法,保留作图痕迹).
(2)连接AP,如果AP平分∠CAB,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知点C在线段AB上,线段AC=6,BC=4,点M、N分别是AC、BC的中点,求MN的长度;
(2)根据(1)的计算过程与结果,设AC+BC=a,其它条件不变,请猜想出MN的长度吗?并说明理由;
(3)对于(1)题,如果将“点C在线段AB上”改为“点C在射线AB上”,其它条件不变,求MN的长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1= ![]() 的图象与一次函数y2=
的图象与一次函数y2= ![]() x的图象交于点A、B,点B的横坐标是4,点P(1,m)在反比例函数y1=
x的图象交于点A、B,点B的横坐标是4,点P(1,m)在反比例函数y1= ![]() 的图象上.
的图象上. 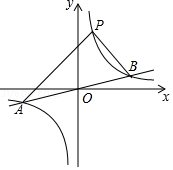
(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
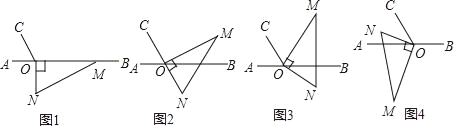
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角尺绕点O逆时针旋转至图2,使点N在OC的反向延长线上,请直接写出图中∠MOB的度数;
(2)将图1中的三角尺绕点O逆时针旋转至图3,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;
(3)将图1中的三角尺绕点O顺时针旋转至图4,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上A、B两点对应的数为0、10,P为数轴上一点
(1)点P为AB线段的中点,点P对应的数为 .
(2)数轴上有点P,使P到A,B的距离之和为20,点P对应的数为 .
(3)若点P点表示6,点M以每秒钟5个单位的速度从A点向右运动,点N以每秒钟1个单位的速度从B点向右运动,t秒后有PM=PN,求时间t的值(画图写过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com