
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+5��x�ύ��A��1��0����B��5��0�����㣬��D���������Ϻ�����Ϊ6�ĵ㣮��P�������������ϣ��Ҳ���A��D�����غϣ�����P��y���ƽ����������AD���ڵ�Q������Q��QF��ֱ��y�ᣬ��F�ڵ�Q���Ҳ࣬��QF=2����QF��QPΪ�ڱ�������QPEF�������QPEF���ܳ�Ϊd����P�ĺ�����Ϊm��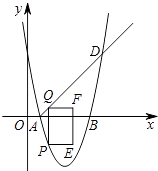
��1������������������Ӧ�ĺ�������ʽ��
��2�������������ߵĶԳ��Ὣ����QPEF�������Ϊ1��2������ʱm��ֵ��
��3����d��m֮��ĺ�����ϵʽ��d��m���������Сʱd��ȡֵ��Χ��
��4��������QPEF�ĶԽ����ഹֱʱ��ֱ��д����Գ����ĵĺ����꣮
���𰸡�
��1��
�⣺��A��1��0����B��5��0������y=ax2+bx+5��
![]() ��
��
��� ![]() ��
��
��y=x2��6x+5
��2��
�⣺��ͼ��ʾ����������y=x2��6x+5�ĶԳ���Ϊ��x=�� ![]() =��
=�� ![]() =3��
=3��
�����������ߵĶԳ��Ὣ����QPEF�������Ϊ1��2�����֣�
�ɵ�PN=3��m��PE=2��
�� ![]() =
= ![]() ��
�� ![]() =
= ![]() ��
��
��ã�m= ![]() ��m=
��m= ![]()

��3��
�⣺��x=6ʱ��y=x2��6x+5=62��6��6+5=5��
���D��������6��5����
����AD����Ӧ�ĺ�������ʽΪy=x��1��x��1����
��P��m��m2��6m+5����Q��m��m��1����
��1��m��6ʱ��d=2����m2+7m��6+2��=��2m2+14m��8��
��m��6ʱ��d=2��m2��7m+6+2��=2m2��14m+16��
��d=��2m2+14m��8=��2��m�� ![]() ��2+
��2+ ![]() ��
��
��d��m���������Сʱd��ȡֵ��Χ��4��d�� ![]()
��4��
�⣺������QPEF�ĶԽ����ഹֱʱ�������QPEF�������Σ��߳�Ϊ2��
��1��m��6ʱ��m��1����m2��6m+5��=2��
�����ã�m2��7m+8=0��
��ã�m1= ![]() ��m2=
��m2= ![]() ��
��
��m��6ʱ��m2��6m+5����m��1��=2��
�����ã�m2��7m+4=0��
��ã�m3= ![]() ��m4=
��m4= ![]() ����ȥ����
����ȥ����
����Գ����ĵĺ�����Ϊ�� ![]() +1=
+1= ![]() ��
�� ![]() +1=
+1= ![]() ��
�� ![]() +1=
+1= ![]()
����������1��ֱ�����ô���ϵ����������κ�������ʽ���ɣ���2��������������Գ�������ó�m��ֵ����3���ֱ����õ�1��m��6ʱ��d=2����m2+7m��6+2������m��6ʱ��d=2��m2��7m+6+2�����d��ȡֵ��Χ���ɣ���4��������QPEF�ĶԽ����ഹֱʱ�������QPEF�������Σ��߳�Ϊ2�������ó�m��ֵ����𰸣�
�����㾫�������ն��κ����������ǽ����ĸ�������Ҫ֪�������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ñ߳�Ϊ12cm��������Ӳֽ�������������ӣ�ÿ�����ӵIJ���Ϊ�����Σ�����Ϊ�ȱ���������
��1��ÿ�������� �������Σ� ���ȱ������Σ�
��2��Ӳֽ������ͼ���ַ����ü����ü���߽��ϲ������ã�
A��������6�����棻 B��������4�������5�����森

����19��Ӳֽ�壬�ü�ʱx����A������������B������
�� ��x�Ĵ���ʽ�ֱ��ʾ�ü����IJ���͵���ĸ�����
�� ���ü����IJ���͵���ǡ��ȫ�����꣬���������ٸ����ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У�BC��AC����ACB��90�㣬DΪ����AB��һ�㣬����CD������C���߶�CD�Ĵ���l����ֱ��l�ϣ��ֱ��ڵ�C�������ȡ���߶�CD��ȵ��߶�CE��CF������AE��BF.
(1)����D���߶�AB��ʱ(��D�����A��B�غ�)����ͼ23(a)��
�����㽫ͼ�β���������
���߶�BF��AD����ֱ�ߵ�λ�ù�ϵΪ________���߶�BF��AD��������ϵΪ________��
(2)����D���߶�AB���ӳ�����ʱ����ͼ23(b)��
��(1)�Т��ʵĽ����Ƿ���Ȼ��������������������֤�����������������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1�����ڡ�ABC�У�AD��BC�ߵ����ߣ���A����AE��BC���D����DE��AB���ڵ�E������CE�� 
��1����֤���ı���ADCE��ƽ���ı��Σ�
��2������BE��AC�ֱ���BE��DE���ڵ�F��G����ͼ��2������AC=6����FG�ij��� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ԭ�ͣ���ͼ�٣��ڵ���ֱ��������ABC�У���ACB=90�㣬BC=a������AB�Ƶ�B˳ʱ����ת90��õ��߶�BD������CD������D����BCD��BC���ϵĸ�DE�� ��֤��ABC�ա�BDE���Ӷ��õ���BCD�����Ϊ ![]() ��
��
����̽������ͼ�ڣ���Rt��ABC�У���ACB=90�㣬BC=a������AB�Ƶ�B˳ʱ����ת90��õ��߶�BD������CD���ú�a�Ĵ���ʽ��ʾ��BCD���������˵�����ɣ�
��Ӧ�ã���ͼ�ۣ��ڵ���������ABC�У�AB=AC��BC=a������AB�Ƶ�B˳ʱ����ת90��õ��߶�BD������CD��ֱ��д����BCD����������ú�a�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
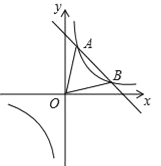
����Ŀ����ͼ��һ�κ���y=kx+b�뷴��������y=![]() ��ͼ����A��1��6����B��3��n�����㣮
��ͼ����A��1��6����B��3��n�����㣮
��1������������һ�κ����ı���ʽ��
��2������ͼ��д������ʽkx+b��![]() ��0�Ľ⼯��
��0�Ľ⼯��
��3������M��x���ϡ���N��y���ϣ�����M��N��A��BΪ������ı�����ƽ���ı��Σ���ֱ��д����M��N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�ա�����������100m���ܵ��������ܲ�ѵ��������ͬʱ���������������յ㣮
��1����С���ٶ�Ϊv��m/s����д��С������ȫ�����õ�ʱ��t��s�����ٶ�v��m/s��֮��ĺ�����ϵʽ��
��2����֪�������ٶ���С���ٶȵ�1.25������������ȫ�̣�С��Ҫ����������4s���÷�ʽ������С�ա��������������ܲ����ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ���ACB=90�㣬AB=4cm������P��1cm/s���ٶȷֱ�ӵ�A��Bͬʱ��������P��A��B���յ�B�˶�����Q��B��A���յ�A�˶�������P��PD��AC�ڵ�D����PDΪ�����Ҳ���������PDEF������Q��QG��AB��������BC��CA�ڵ�G���C���غϣ���QGΪ��������ֱ�ǡ�QGH���ҵ�GΪֱ�Ƕ��㣬��C��Hʼ����QG��ͬ�࣬��������PDEF���QGH�ص�����ͼ�ε����ΪS��cm2������P�˶���ʱ��Ϊt��s����0��t��4����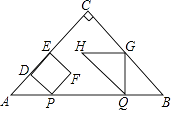
��1������F�ڱ�QH��ʱ����t��ֵ��
��2����������PDEF���QGH�ص�����ͼ�����ı���ʱ����S��t֮��ĺ�����ϵʽ��
��3����FH���ڵ�ֱ��ƽ�л�ֱ��ABʱ��ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʢʢͬѧ��ij��У����ʱ�������˶������������еIJ�����Ϣ�����±�����
Ժϵ�������ɼ����� | |||
�������� | ʤ�� | ���� | ���� |
22 | 12 | 10 | 34 |
22 | 14 | 8 | 36 |
22 | 0 | 22 | 22 |
ʢʢͬѧ���ѧϰ��֪ʶ������������⣬�����æ����������⣺
��1���ӱ��п��Կ�������һ����______��,ʤһ����_______����
��2��ij���ڱ���22����ǰ���£�ʤ���ܻ����ܵ����为���ܻ��ֵ�2������˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com