
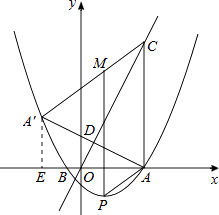
【题目】如图,抛物线y= ![]() x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;
x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;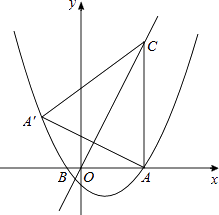
(1)求该抛物线的解析式;
(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵y= ![]() x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,
x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,
∴ 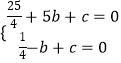 ,
,
解得 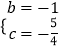 .
.
∴抛物线的解析式为y= ![]() x2﹣x﹣
x2﹣x﹣ ![]()
(2)
解:如答图所示,过点A′作A′E⊥x轴于E,AA′与OC交于点D,
∵点C在直线y=2x上,
∴C(5,10)
∵点A和A′关于直线y=2x对称,
∴OC⊥AA′,A′D=AD.
∵OA=5,AC=10,
∴OC= ![]() =
= ![]() =
= ![]() .
.
∵S△OAC= ![]() OCAD=
OCAD= ![]() OAAC,
OAAC,
∴AD= ![]() .
.
∴AA′= ![]() ,
,
在Rt△A′EA和Rt△OAC中,
∵∠A′AE+∠A′AC=90°,
∠ACD+∠A′AC=90°,
∴∠A′AE=∠ACD.
又∵∠A′EA=∠OAC=90°,
∴Rt△A′EA∽Rt△OAC.
∴ ![]() ,
,
即 ![]() .
.
∴A′E=4,AE=8.
∴OE=AE﹣OA=3.
∴点A′的坐标为(﹣3,4),
当x=﹣3时,
y= ![]() ×(﹣3)2+3﹣
×(﹣3)2+3﹣ ![]() =4.
=4.
所以,点A′在该抛物线上
(3)
解:存在.
理由:设直线CA′的解析式为y=kx+b,
则 ![]() ,
,
解得 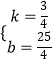
∴直线CA′的解析式为y= ![]() x+
x+ ![]()
设点P的坐标为(x, ![]() x2﹣x﹣
x2﹣x﹣ ![]() ),则点M为(x,
),则点M为(x, ![]() x+
x+ ![]() ).
).
∵PM∥AC,
∴要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,
∴( ![]() x+
x+ ![]() )﹣(
)﹣( ![]() x2﹣x﹣
x2﹣x﹣ ![]() )=10.
)=10.
解得x1=2,x2=5(不合题意,舍去)
当x=2时,y=﹣ ![]() .
.
∴当点P运动到(2,﹣ ![]() )时,四边形PACM是平行四边形
)时,四边形PACM是平行四边形
【解析】方法一:(1)利用待定系数法求出抛物线的解析式;(2)首先求出对称点A′的坐标,然后代入抛物线解析式,即可判定点A′是否在抛物线上.本问关键在于求出A′的坐标.如答图所示,作辅助线,构造一对相似三角形Rt△A′EA∽Rt△OAC,利用相似关系、对称性质、勾股定理,求出对称点A′的坐标;(3)本问为存在型问题.解题要点是利用平行四边形的定义,列出代数关系式求解.如答图所示,平行四边形的对边平行且相等,因此PM=AC=10;利用含未知数的代数式表示出PM的长度,然后列方程求解.
【考点精析】掌握二次函数的性质是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】已知数轴上点A对应的数是20,点B对应的数是﹣30,甲从A点出发以每秒1个单位长度的速度匀速运动,乙从B出发以每秒3个长度单位的速度匀速运动,若甲乙两人同时出发
(1)若甲和乙在数轴上运动3秒后,
①它们相距最远时,甲所在的位置对应的数是 ,乙所在的位置对应的数是
②它们距离最近时,甲所在的位置对应的数是 ,乙所在的位置对应的数是
(2)若甲和乙同时向右,出发多少秒后,甲和乙相距20个长度单位?
(3)若甲和乙进行匀速往返跑训练,甲从A点起跑,到达B点后,立即转身跑向A点,到达A点后,又立即转身跑向B点……;乙从B点起跑,到达A点后,立即转身跑向B点,到达B点后,又立即转身跑向A点……;两人同时出发,问:起跑后两人第二次相遇的时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式![]() ,当
,当![]() 时,该代数式的值为3.
时,该代数式的值为3.
(1)求c的值;
(2)已知:当![]() 时,该代数式的值为0.
时,该代数式的值为0.
①求:当![]() 时,该代数式的值;
时,该代数式的值;
②若![]() ,
,![]() ,
,![]() ,试比较a与d的大小,并说明理由.
,试比较a与d的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元(m>n)的价格进了同样的60包茶叶,如果商家以每包![]() 元的价格卖出这种茶叶,卖完后,这家商店( )
元的价格卖出这种茶叶,卖完后,这家商店( )
A.盈利了 B.亏损了 C.不赢不亏 D.盈亏不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α, 以OC为边作等边三角形OCD,连接AD.

(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当a为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
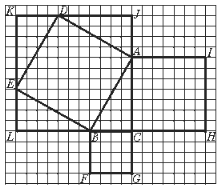
【题目】在两千多年前我国古算术上记载有“勾三股四弦五”.你知道它的意思吗?
它的意思是说:如果一个直角三角形的两条直角边长分别为3和4个长度单位,那么它的斜边的长一定是5个长度单位,而且3、4、5这三个数有这样的关系:32+42=52.
(1)请你动动脑筋,能否验证这个事实呢?该如何考虑呢?
(2)请你观察下列图形,直角三角形ABC的两条直角边的长分别为AC=7,BC=4,请你研究这个直角三角形的斜边AB的长的平方是否等于42+72?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学要在操场的一块长方形土地上进行绿化,已知这块长方形土地的长为5![]() m,宽为4
m,宽为4![]() m.
m.
(1)求该长方形土地的面积(精确到0.1 m2);
(2)如果绿化该长方形土地每平方米的造价为180元,那么绿化该长方形土地所需资金约为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上两定点A、B对应的数分别为-18和14,现在有甲、乙两只电子蚂蚁分别从A、B同时出发,沿着数轴爬行,速度分别为每秒1.5个单位和1.7个单位,它们第一次相向爬行1秒,第二次反向爬行2秒,第三次相向爬行3秒,第四次反向爬行4秒,第五次相向爬行5秒,……,按如此规律,则它们第一次相遇所需的时间为( )

A. 55秒 B. 190秒 C. 200秒 D. 210秒
查看答案和解析>>
科目:初中数学 来源: 题型:
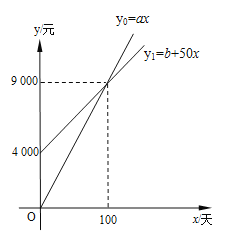
【题目】国家推行“节能减排,低碳经济”政策后,某企业推出一种“CNG”改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0,y1(元)与正常运营时间x(天)之间分别满足关系式:y0=ax,y1=b+50x,图象如图所示.
(1)每辆车改装前每天的燃料费a= 元,每辆车的改装费b= 元,正常运营时间 天后,就可以从节省的燃料费中收回改装成本;
(2)某出租汽车公司一次性改装了100辆出租车,因而正常运行多少天后共节省燃料费40万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com