
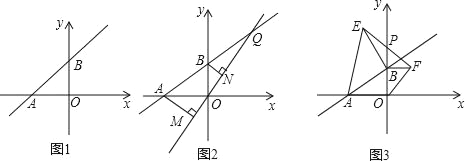
����Ŀ����ͼ1��ֱ��l��y=mx+10m��x�Ḻ���ᡢy��������ֱ���A��B���㣮
��1����OA=OBʱ����ȷ��ֱ��l�ĺ�������ʽ��
��2���ڣ�1���������£���ͼ2����QΪֱ��AB��һ�㣬��ֱ��OQ����A��B����ֱ���AM��OQ��M��BN��OQ��N����AM=8��BN=6����MN�ij���
��3����mȡ��ͬ��ֵʱ����B��y�����������˶����ֱ���OB��ABΪ�ߣ���BΪֱ�Ƕ����ڵ�һ����������������ֱ����OBF�͵���ֱ����ABE����EF��y����P�㣬��ͼ3���ʣ�����B�� y�����������˶�ʱ���Բ���PB�ij��Ƿ�Ϊ��ֵ�����ǣ��������ֵ�������ǣ�˵�����ɣ�
���𰸡���1��y=x+10����2��14����3��PB�ij�Ϊ��ֵ�����ɼ�����.
��������
���⣨1����y=0�����x=��10���Ӷ�����õ�A�����꣬��x=0��y=10m����OA=OB��֪��B��������Ϊ10���Ӷ������m��ֵ��
��2������AAS֤����AMO�ա�ONB����ȫ�������ε����ʿ�֪ON=AM��OM=BN�������MN=AM+BN�����MN�ij���
��3������E��EG��y����G�㣬��֤����ABO�ա�EGB���Ӷ��õ�BG=10��Ȼ��֤����BFP�ա�GEP���Ӷ��õ�BP=GP=BG��
�⣺��1��������֪��A����10��0����B��0��10m��
��OA=OB��
��10m=10����m=1��
��L�Ľ���ʽy=x+10��
��2����AM��OQ��BN��OQ
���AMO=��BNO=90��
���AOM+��MAO=90��
�ߡ�AOM+BON=90��
���MAO=��NOB
����AMO����ONB��
![]() ��
��
���AMO�ա�ONB��
��ON=AM��OM=BN��
��AM=8��BN=6��
��MN=AM+BN=14��
��3��PB�ij�Ϊ��ֵ��
���ɣ���ͼ��ʾ������E��EG��y����G�㣮
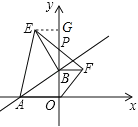
�ߡ�AEBΪ����ֱ�������Σ�
��AB=EB����ABO+��EBG=90����
��EG��BG��
���GEB+��EBG=90����
���ABO=��GEB��
����ABO����EGB��
![]() ��
��
���ABO�ա�EGB��
��BG=AO=10��OB=EG
�ߡ�OBFΪ����ֱ�������Σ�
��OB=BF
��BF=EG��
����BFP����GEP��
![]() ��
��
���BFP�ա�GEP��
��BP=GP=BG=5��


 ÿ�α���ϵ�д�
ÿ�α���ϵ�д� ��ѧ����ϵ�д�
��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���û��������з�ʽ������Σ�
![]() ��
��
(1)�����
������� | 1 | 2 | 3 | 4 | �� |
�������� | �� |
(2)�������εĸ���Ϊnʱ�������ĸ����Ƕ��٣�
(3)��n��1 000ʱ�������ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����O�ǵȱ�������ABC��һ�㣬��AOB=110������BOC=��, ��OCΪ�����ȱ�������OCD������AD.

��1������=150��ʱ�����ж���AOD����״����˵�����ɣ�
��2��̽������aΪ���ٶ�ʱ����AOD�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧҪ�ڲٳ���һ�鳤���������Ͻ����̻�����֪��鳤�������صij�Ϊ5![]() m����Ϊ4
m����Ϊ4![]() m.
m.
(1)��ó��������ص����(��ȷ��0.1 m2)��
(2)����̻��ó���������ÿƽ�������Ϊ180Ԫ����ô�̻��ó��������������ʽ�ԼΪ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ڰ�ȫ�������У������ˡ�����Ȼ�ֺ�������֪ʶ֪���١�ר���������ȡ��������ķ�ʽ�����ʾ����飬�ʾ�����Ľ����Ϊ���dz��˽⡱�����Ƚ��˽⡱���������˽⡱������̫�˽⡱�ĸ��ȼ������۵ȼ���������������±���
�ȼ� | �dz��˽� | �Ƚ��˽� | �����˽� | ��̫�˽� |
Ƶ�� | 40 | 120 | n | 4 |
Ƶ�� | 0.2 | m | 0.18 | 0.02 |
��1������m��ֵΪ �� n��ֵΪ��
��2�����ݱ��е����ݣ�������㡰�dz��˽⡱��Ƶ������ͼ�ж�Ӧ�����ε�Բ�ĽǵĶ���������ȫ����ͳ��ͼ�� 
��3����Уһ����2400��ѧ��������ݵ���������ȫУѧ���С��Ƚ��˽⡱������Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������������A��B��Ӧ�����ֱ�Ϊ��18��14�������мס�����ֻ�������Ϸֱ��A��Bͬʱ�����������������У��ٶȷֱ�Ϊÿ��1��5����λ��1��7����λ�����ǵ�һ����������1�룬�ڶ��η�������2�룬��������������3�룬���Ĵη�������4�룬�������������5�룬����������˹��ɣ������ǵ�һ�����������ʱ��Ϊ�� ��

A. 55�� B. 190�� C. 200�� D. 210��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����EΪ��AC���ӳ�����һ�㣬DE���O�����ڵ�D����DE��AC������OD����AB=10��AC=6����DE�ij��� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���á�������������������գ�
��1����![]() _____��
_____��![]() ��
��
��2��������0.01��_____ ����![]() ��2��
��2��
��3��3.9950����ȷ��0.01��_____3.999��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����MΪֱ��AB��һ���㣬 ![]() ���ǵȱ������Σ�����BN
���ǵȱ������Σ�����BN
![]() ��֤��
��֤�� ![]() ��
��
![]() �ֱ�д����M����ͼ2��ͼ3��ʾλ��ʱ���߶�AB��BM��BN����֮���������ϵ
�ֱ�д����M����ͼ2��ͼ3��ʾλ��ʱ���߶�AB��BM��BN����֮���������ϵ![]() ����֤��
����֤��![]() ��
��
![]() ��ͼ4����
��ͼ4����![]() ʱ��֤����
ʱ��֤���� ![]() ��
��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com