
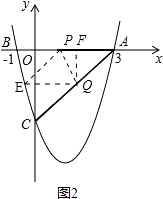
【题目】如图1(注:与图2完全相同),二次函数y= ![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.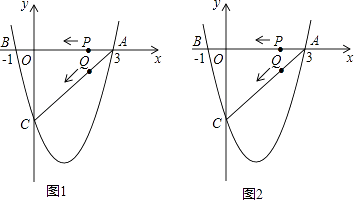
(1)求该二次函数的解析式;
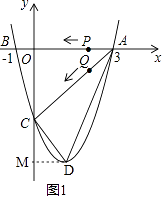
(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).
【答案】
(1)
解:∵二次函数y= ![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),
∴ 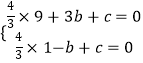 ,
,
解得: 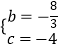 ,
,
∴y= ![]() x2﹣
x2﹣ ![]() x﹣4
x﹣4
(2)
解:过点D作DM⊥y轴于点M,
∵y= ![]() x2﹣
x2﹣ ![]() x﹣4=
x﹣4= ![]() (x﹣1)2﹣
(x﹣1)2﹣ ![]() ,
,
∴点D(1,﹣ ![]() )、点C(0,﹣4),
)、点C(0,﹣4),
则S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC
= ![]() ×(1+3)×
×(1+3)× ![]() ﹣
﹣ ![]() ×(
×( ![]() ﹣4)×1﹣
﹣4)×1﹣ ![]() ×3×4
×3×4
=4
(3)
解:四边形APEQ为菱形,E点坐标为(﹣ ![]() ,﹣
,﹣ ![]() ).理由如下
).理由如下
如图2,E点关于PQ与A点对称,过点Q作,QF⊥AP于F,
∵AP=AQ=t,AP=EP,AQ=EQ
∴AP=AQ=QE=EP,
∴四边形AQEP为菱形,
∵FQ∥OC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]()
∴AF= ![]() t,FQ=
t,FQ= ![]() t
t
∴Q(3﹣ ![]() t,﹣
t,﹣ ![]() t),
t),
∵EQ=AP=t,
∴E(3﹣ ![]() t﹣t,﹣
t﹣t,﹣ ![]() t),
t),
∵E在二次函数y= ![]() x2﹣
x2﹣ ![]() x﹣4上,
x﹣4上,
∴﹣ ![]() t=
t= ![]() (3﹣
(3﹣ ![]() t)2﹣
t)2﹣ ![]() (3﹣
(3﹣ ![]() t)﹣4,
t)﹣4,
∴t= ![]() ,或t=0(与A重合,舍去),
,或t=0(与A重合,舍去),
∴E(﹣ ![]() ,﹣
,﹣ ![]() ).
).
【解析】(1)将A,B点坐标代入函数y= ![]() x2+bx+c中,求得b、c,进而可求解析式;(2)由解析式先求得点D、C坐标,再根据S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC , 列式计算即可;(3)注意到P,Q运动速度相同,则△APQ运动时都为等腰三角形,又由A、E对称,则AP=EP,AQ=EQ,易得四边形四边都相等,即菱形.利用菱形对边平行且相等的性质可用t表示E点坐标,又E在二次函数的图象上,所以代入即可求t,进而E可表示.
x2+bx+c中,求得b、c,进而可求解析式;(2)由解析式先求得点D、C坐标,再根据S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC , 列式计算即可;(3)注意到P,Q运动速度相同,则△APQ运动时都为等腰三角形,又由A、E对称,则AP=EP,AQ=EQ,易得四边形四边都相等,即菱形.利用菱形对边平行且相等的性质可用t表示E点坐标,又E在二次函数的图象上,所以代入即可求t,进而E可表示.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图所示,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α, 以OC为边作等边三角形OCD,连接AD.

(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当a为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“<”“>”或“=”号填空:
(1)﹣![]() _____﹣
_____﹣![]() ;
;
(2)﹣(﹣0.01)_____ (﹣![]() )2;
)2;
(3)3.9950(精确到0.01)_____3.999.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…
(1)请根据你发现的规律填空:6×8+1=( )2;
(2)用含n的等式表示上面的规律: ;
(3)用找到的规律解决下面的问题:
计算:(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
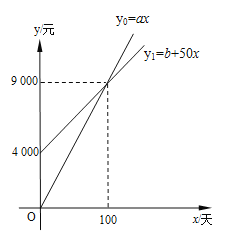
【题目】国家推行“节能减排,低碳经济”政策后,某企业推出一种“CNG”改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0,y1(元)与正常运营时间x(天)之间分别满足关系式:y0=ax,y1=b+50x,图象如图所示.
(1)每辆车改装前每天的燃料费a= 元,每辆车的改装费b= 元,正常运营时间 天后,就可以从节省的燃料费中收回改装成本;
(2)某出租汽车公司一次性改装了100辆出租车,因而正常运行多少天后共节省燃料费40万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温度的度量有两种基本单位:摄氏温度(℃),华氏温度(℉).在温度计上,摄氏温度x与华氏温度y有如下表所示的对应关系:
x/℃ | … | -10 | 0 | 10 | 20 | … |
y/℉ | … | 14 | 32 | 50 | 68 | … |
按下列步骤确定y与x之间的函数关系式.
(1)在平面直角坐标系中描点、连线,画出图象;
(2)猜想能表示y与x之间关系的函数类型;
(3)确定y与x之间的函数关系式,并验证你的想法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点, ![]() 都是等边三角形,连接BN
都是等边三角形,连接BN
![]() 求证:
求证: ![]() ;
;
![]() 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系![]() 不需证明
不需证明![]() ;
;
![]() 如图4,当
如图4,当![]() 时,证明:
时,证明: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(2,0),B(1,m2﹣4m+5).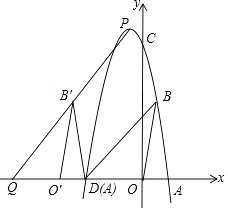
(1)直接判断△ABO是什么图形;
(2)如果S△ABO有最小值,求m的值;
(3)抛物线y=﹣(x﹣2)(x﹣n)经过点B且与y轴交于点C,与x轴交于两点A,D.
①用含m的式子表示点C和点D坐标;
②点P是抛物线上x轴上方任一点,PQ∥BD交x轴于点Q,将△ABO向左平移到△A′B′O′,点A,B,O的对应点分别是A′,B′,O′,当点A'与点D重合时,点B'在线段PQ上,如果点P恰好是抛物线顶点,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com