
����Ŀ����ͼ����֪A��2��0����B��1��m2��4m+5����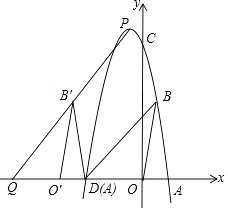
��1��ֱ���жϡ�ABO��ʲôͼ�Σ�
��2�����S��ABO����Сֵ����m��ֵ��
��3��������y=����x��2����x��n��������B����y�ύ�ڵ�C����x�ύ������A��D��
���ú�m��ʽ�ӱ�ʾ��C�͵�D���ꣻ
�ڵ�P����������x���Ϸ���һ�㣬PQ��BD��x���ڵ�Q������ABO����ƽ�Ƶ���A��B��O�䣬��A��B��O�Ķ�Ӧ��ֱ���A�䣬B�䣬O�䣬����A'���D�غ�ʱ����B'���߶�PQ�ϣ������Pǡ���������߶��㣬��m��ֵ��
���𰸡�
��1��
�⣺��A��2��0����B��1��m2��4m+5����
���B���߶�OA�Ĵ�ֱƽ�����ϣ�
��OB=AB��
���ABO �ǵ���������
��2��
�⣺��S��ABO= ![]() ��2����m2��4m+5��=m2��4m+5=��m��2��2+1��
��2����m2��4m+5��=m2��4m+5=��m��2��2+1��
�൱m=2ʱ��S��ABO ����Сֵ
��3��
�⣺�ٰ�B��1��m2��4m+5������
y=����x��2����x��n����m2��4m+5=����1��2����1��n����
��n=����m��2��2��
��y=��x2+����m2+4m��2��x+2��m��2��2��
��x=0����y=2��m��2��2��
��C��0��2��m��2��2����
��D������m��2��2��0����
�ڡ�B��1��m2��4m+5����D������m��2��2��0����
��ֱ��DB�Ľ���ʽΪy=x+��m��2��2��
��B'������m��2��2��1����m��2��2+1 ����
��ֱ��PQ�Ľ���ʽΪy=x+2��m��2��2+2��
�߶���P�� ![]() ��2��m��2��2+
��2��m��2��2+ ![]() ����
����
��P����ֱ��PQ�ϣ�
��2��m��2��2+ ![]() ��=
��= ![]() +2��m��2��2+2��
+2��m��2��2+2��
��n=����m��2��2��
��n2+2n��8=0
��n=����m��2��2��
��n2+2n��8=0��
���n1=2��n2=��4��
�ੁ��m��2��2=2����ȥ����m��2��2=4��
��m1=4��m2=0
����������1����B��������֪��B���߶�OA�Ĵ�ֱƽ�����ϣ���֪OB=AB���ɵó��𰸣���2����m�ɱ�ʾ����ABO����������ö��κ��������ʿ������ȡ����Сֵʱ��m��ֵ����3���ٰ�B��������������߽���ʽ����m��ʾ��n��ֵ��������C��D�����ꣻ����B��D����ɱ�ʾ��ֱ��BD����ʽ����ƽ�ƿɱ�ʾ��B������꣬�Ӷ�����m��ʾ��ֱ��PQ�Ľ���ʽ������m��ʾ��P�����꣬����ֱ��PQ����ʽ����ɵõ�����m�ķ��̣������m��ֵ��
�����㾫����������Ҫ�����˶��κ�������ֵ�����֪ʶ�㣬��Ҫ��������Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ע����ͼ2��ȫ��ͬ�������κ���y= ![]() x2+bx+c��ͼ����x�ύ��A��3��0����B����1��0�����㣬��y�ύ�ڵ�C��
x2+bx+c��ͼ����x�ύ��A��3��0����B����1��0�����㣬��y�ύ�ڵ�C��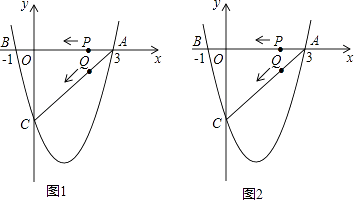
��1����ö��κ����Ľ���ʽ��
��2����������ߵĶ���ΪD�����ACD�����������ͼ1��̽������
��3������P��Qͬʱ��A�����������ÿ��1����λ���ȵ��ٶȷֱ���AB��AC���˶�������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶�����P��Q�˶���t��ʱ����APQ��PQ���ڵ�ֱ�߷��ۣ���Aǡ��������������E�㴦����ֱ���ж���ʱ�ı���APEQ����״�������E�����꣨����ͼ2��̽������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
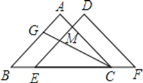
����Ŀ����ͼ����E��C��BF�ϣ�![]() ��
��![]() ��
��![]() ��
��
![]() ��֤��
��֤��![]() ��
��
![]() ��AC��DE��M����
��AC��DE��M����![]() ��
��![]() �����߶�CE�Ƶ�C˳ʱ����ת��ʹ��E��ת��AB�ϵ�G��������ת��
�����߶�CE�Ƶ�C˳ʱ����ת��ʹ��E��ת��AB�ϵ�G��������ת��![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵��ڽ����ڼ俪չ�Żݴ����������ԭ�۳���200Ԫ����Ʒ������200Ԫ�IJ��ֿ������ܴ����Żݣ���������Ʒ��ʵ�ʸ�����y����λ��Ԫ������Ʒԭ��x����λ��Ԫ���ĺ�����ϵ��ͼ����ͼ��ʾ����200Ԫ�IJ��ֿ������ܵ��Ż��ǣ�������

A. ������ B. ������ C. ������ D. �����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���BAD=120�㣬��������EF�۵�����B��������AD�ߵĵ�G������EG��AC����CD=8����FG�ij�Ϊ�� �� 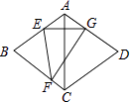
A.4 ![]()
B.4 ![]()
C.4 ![]()
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ��AB��һ��OΪ�˵������� OC��ʹ��BOC=60�㣬��һ��ֱ�������ε�ֱ�Ƕ�����ڵ�O������ע����DOE=90�㣩
��1����ͼ1����ֱ�����ǰ�DOE��һ��OD��������OB��������COE= �㣻
��2����ͼ2����ֱ�����ǰ�DOE�Ƶ�O��ʱ�뷽��ת����ij��λ������OEǡ��ƽ����AOC����˵��OD������������BOC��ƽ������
��3����ͼ3�������ǰ�DOE�Ƶ�O��ʱ��ת����ij��λ��ʱ����ǡ����COD= ![]() ��AOE������BOD�Ķ�����
��AOE������BOD�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ȥ�ľ���Ʒ�̵��ͬѧ��ijƷ��ˮ�Աʣ���֪�ס������̵궼�и�Ʒ�Ƶ�ˮ�Ա��ұ�۶���2Ԫ/֧�����ס������̵���Ż�����ȴ��ͬ��
���̵꣺��������10֧����۸����һ�ι�10֧���ϣ���10֧�IJ��ְ���۵�60%��� ���̵꣺����۵�80%���
��ˮ�Աʵ�������������ͬ�������£�
��1����С��Ҫ����ĸ�Ʒ�Ʊ�����x��x��10��֧�����ú�x��ʽ�ӷֱ��ʾ�ڼס��������̵깺���Ʒ�Ʊ���ˮ�Աʵķ��ã�
��2����С��Ҫ�����Ʒ�Ʊ�30֧������Ϊ�ڼס������̵��У����ĸ��̵깺��Ƚ�ʡǮ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
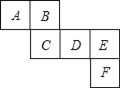
����Ŀ����ͼ��һ��������ı���չ��ͼ����ش��������⣺
��1������B��C��Ե���ֱ����� ����
��2����A��a3+a2b+3��B��a2b��3��C��a3��1��D������a2b��6�������������������ʾ�Ĵ���ʽ�ĺͶ���ȣ���E��F�ֱ�����Ĵ���ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com