
【题目】如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,且点E在线段AD上,若AF=4,∠F=60°.
(1)指出旋转中心和旋转角度;
(2)求DE的长度和∠EBD的度数.
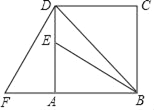
【答案】(1) 90°;(2) 15°.
【解析】
试题(1)由于△ADF旋转一定角度后得到△ABE,根据旋转的性质得到旋转中心为点A,∠DAB等于旋转角,于是得到旋转角为90°;(2)根据旋转的性质得到AE=AF=4,∠AEB=∠F=60°,则∠ABE=90°﹣60°=30°,解直角三角形得到AD=4![]() ,∠ABD=45°,所以DE=4
,∠ABD=45°,所以DE=4![]() ﹣4,然后利用∠EBD=∠ABD﹣∠ABE计算即可.
﹣4,然后利用∠EBD=∠ABD﹣∠ABE计算即可.
试题解析:(1)∵△ADF旋转一定角度后得到△ABE,
∴旋转中心为点A,∠DAB等于旋转角,
∴旋转角为90°;
(2)∵△ADF以点A为旋转轴心,顺时针旋转90°后得到△ABE,
∴AE=AF=4,∠AEB=∠F=60°,
∴∠ABE=90°﹣60°=30°,
∵四边形ABCD为正方形,
∴AD=AB=4![]() ,∠ABD=45°,
,∠ABD=45°,
∴DE=4![]() ﹣4,
﹣4,
∠EBD=∠ABD﹣∠ABE=15°.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,AB为⊙O的直径,AC的延长线上有点D,AC=3CD,连接BD,E为BD的中点,CE是⊙O的切线.
(1)求证:BD与⊙O相切;
(2)求∠ACE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现,
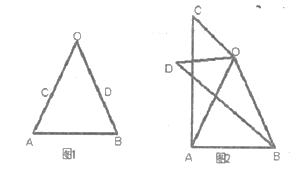
如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,将点
上一点,将点![]() 绕点
绕点![]() 顺时针旋转50°得到点
顺时针旋转50°得到点![]() ,则
,则![]() 与
与![]() 的数量关系是________________________。
的数量关系是________________________。
(2)类比探究
如图2,将(1)中的![]() 绕点
绕点![]() 在平面内旋转,(1)中的结论是否成立,并就图2的情形说明理由。
在平面内旋转,(1)中的结论是否成立,并就图2的情形说明理由。
(3)拓展延伸
![]() 绕点
绕点![]() 在平面旋转,当旋转到
在平面旋转,当旋转到![]() 时,请直接写出
时,请直接写出![]() 度数。
度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板的两个直角顶点叠放在一起拼成如下的图形.若∠EAB=40°,则∠CAD=____;将△ABC绕直角顶点A旋转时,保持AD在∠BAC的内部,设∠EAC=x°,∠BAD=y°,则x与y的关系是_______.
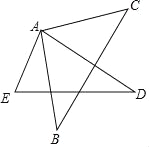
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品的进价为每件30元,销售过程中发现月销售量y(件)与销售单价x(元)之间的关系如图所示.
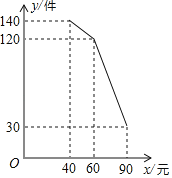
(1)根据图象直接写出y与x之间的函数关系式.
(2)设这种商品月利润为W(元),求W与x之间的函数关系式.
(3)这种商品的销售单价定为多少元时,月利润最大?最大月利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
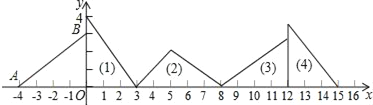
【题目】如图,在平面直角坐标系中,已知点A(﹣4,0)、B(0,3),对△AOB连续作旋转变换依次得到三角形(1)、(2)、(3)、(4)、…,则第(5)个三角形的直角顶点的坐标是_____,第(2018)个三角形的直角顶点的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知命题“等腰三角形两腰上的高线长相等”
(1)请写出该命题的逆命题;
(2)判断(1)中命题的真假,并画出图形,补充已知,求证,及证明过程.
图形:
已知:在△ABC中,CD⊥AB,BE⊥AC,且______.
求证:______.
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是经过∠BCA的顶点C的一条直线,CA=CB,E,F是直线CD上的两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图(a),若∠BCA=90°,α=90°,则BE________CF,EF________|BE-AF|(填“>”“<”或“=”);
②如图(b),若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件________,使①中的两个结论仍然成立,并证明两个结论成立;
(2)如图(c),若直线CD经过∠BCA的外部,∠BCA=α,请写出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com