
【题目】如图,已知△ABC内接于⊙O,AB为⊙O的直径,AC的延长线上有点D,AC=3CD,连接BD,E为BD的中点,CE是⊙O的切线.
(1)求证:BD与⊙O相切;
(2)求∠ACE的度数.

【答案】(1)详见解析;(2)120°
【解析】
(1)连接OC,如图,利用圆周角定理得∠ACB=90°,再根据斜边上的中线性质得CE=BE=DE,所以∠1=∠2,接着根据切线的性质得∠1+∠3=90°,于是∠2+∠4=90°,然后根据切线的判定定理得到结论;
(2)设CD=x,则AC=3x,先证明△ABC∽△ADB,利用相似比得到AB=2![]() x,然后在Rt△ACB中利用余弦定义求出∠A=30°,则∠OCA=∠A=30°,从而得到∠ACE的度数.
x,然后在Rt△ACB中利用余弦定义求出∠A=30°,则∠OCA=∠A=30°,从而得到∠ACE的度数.
(1)连接OC,如图,
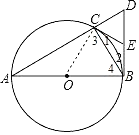
∵AB为⊙O的直径,
∴∠ACB=90°,
∵E为BD的中点,
∴CE=BE=DE,
∴∠1=∠2,
∵OB=OC,
∴∠3=∠4,
∵CE是⊙O的切线.
∴OC⊥CE,
∴∠1+∠3=90°,
∴∠2+∠4=90°,即∠OBE=90°,
∴BD⊥AB,
∴BD与⊙O相切;
(2)解:设CD=x,则AC=3x,
∵∠CAB=∠BAD,∠ACB=∠ABD=90°,
∴△ABC∽△ADB,
∴![]() ,即
,即![]() ,
,
∴AB=2![]() x,
x,
在Rt△ACB中,∵cosA=![]() =
=![]() ,
,
∴∠A=30°,
∵OA=OC,
∴∠OCA=∠A=30°,
∴∠ACE=30°+90°=120°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图(1),在![]() 和
和![]() 中,
中,![]() 为
为![]() 边
边![]() 上一点,
上一点,![]() 平分
平分![]() ,
,![]() ,
,![]() .
.

(1)求证:![]()
(2)如图(2),若![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,
,![]() 为边
为边![]() 上一点,满足
上一点,满足![]() ,连接
,连接![]() 交
交![]() 于
于![]() . ①求
. ①求![]() 的度数;
的度数;
②若![]() 平分
平分![]() ,试说明:
,试说明:![]() 平分
平分![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上的一个动点,过点
边上的一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的平
的平
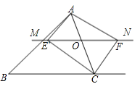
分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 当点
当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?为什么?
是矩形?为什么?
![]() 进行怎样的变化才能使
进行怎样的变化才能使![]() 边上存在点
边上存在点![]() ,使四边形
,使四边形![]() 是正方形?为什么?
是正方形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动漫节开幕前,某动漫公司预测某种动漫玩具能够畅销,就分两批分别用32000元和68000元购进了这种玩具销售,其中第二批购进数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该动漫公司这两批各购进多少套玩具?
(2)如果这两批玩具每套售价相同,且全部销售后总利润不少于20000元,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α, 以OC为边作等边三角形OCD,连接AD.

(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当a为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE,若AE=AB,则∠EBC的度数为( )
中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE,若AE=AB,则∠EBC的度数为( )
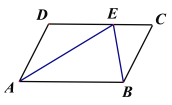
A.30°B.50°C.80°D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转角
顺时针旋转角![]() 得
得![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点.
两点.
![]() 如图
如图![]() ,观察并猜想:图中在不连接其它线段的情况下,共有多少对全等三角形(不包含
,观察并猜想:图中在不连接其它线段的情况下,共有多少对全等三角形(不包含![]() )?将它们全部写出来,并且选一组全等三角形进行证明;
)?将它们全部写出来,并且选一组全等三角形进行证明;
![]() 如图
如图![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
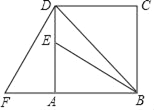
【题目】如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,且点E在线段AD上,若AF=4,∠F=60°.
(1)指出旋转中心和旋转角度;
(2)求DE的长度和∠EBD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com