
【题目】在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转角
顺时针旋转角![]() 得
得![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点.
两点.
![]() 如图
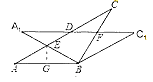
如图![]() ,观察并猜想:图中在不连接其它线段的情况下,共有多少对全等三角形(不包含
,观察并猜想:图中在不连接其它线段的情况下,共有多少对全等三角形(不包含![]() )?将它们全部写出来,并且选一组全等三角形进行证明;
)?将它们全部写出来,并且选一组全等三角形进行证明;
![]() 如图
如图![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.

【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)因为AB=BC,由旋转的性质可知,∠A=∠C=∠C1,AB=BC=BC1,∠ABE=∠C1BF,可证△ABE≌△C1BF;由△ABE≌△C1BF得BE=BF,故AE=ABBE=BCBF=CF,∠A1=∠C,可证△DAE≌△DCF;由△DAE≌△DCF得DE=DF,及BE=BF,BD=BD,可证△DEB≌△DFB;由A1B=BC,A1D=DC,BD=BD,可证△ABD≌△C1BD;同理可证△A1BD≌△CBD.
(2)当a=30°时,在△ABE中,∠A=∠EBA=30°,AB=2,作EG⊥AB,垂足为G,解直角三角形求BE.
共![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
证明:∵AB=BC,
∴∠A=∠C,
由旋转可知,AB=BC1,∠A=∠C1,∠ABE=∠C1BF,
∴△ABE≌△C1BF;
![]() 当
当![]() 时,如图,作
时,如图,作![]() ,垂足为
,垂足为![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】![]() 年是我国实现第一个百年目标,全国建成小康社会的收官之年,早在十六大我党就提出加快推进社会主义现代化,力争国民生产总值到
年是我国实现第一个百年目标,全国建成小康社会的收官之年,早在十六大我党就提出加快推进社会主义现代化,力争国民生产总值到![]() 年比
年比![]() 年翻两番,要实现这一目标,以十年为单位计算,求每十年的国民生产总值的增长率是多少?
年翻两番,要实现这一目标,以十年为单位计算,求每十年的国民生产总值的增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,AB为⊙O的直径,AC的延长线上有点D,AC=3CD,连接BD,E为BD的中点,CE是⊙O的切线.
(1)求证:BD与⊙O相切;
(2)求∠ACE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.

(1)求证:AE=EF;
(2)如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,(1)中的结论是否仍然成立? ;(填“成立”或“不成立”);
(3)如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请证明,若不成立说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2﹣2x+3用配方法化成y=a(x﹣h)2+k的形式是________,抛物线与x轴的交点坐标是________,抛物线与y轴的交点坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 为锐角.点
为锐角.点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() ,以
,以![]() 为一边且在
为一边且在![]() 的右侧作正方形
的右侧作正方形![]() .
.
解答下列问题:
![]() 如果
如果![]() ,
,![]() .
.
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),如图2,线段
不重合),如图2,线段![]() 、
、![]() 之间的位置关系为________,数量关系为________.
之间的位置关系为________,数量关系为________.
②当点![]() 在线段
在线段![]() 的延长线上时,如图3,①中的结论是否仍然成立,为什么?
的延长线上时,如图3,①中的结论是否仍然成立,为什么?
![]() 如果
如果![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动.试探究:当
上运动.试探究:当![]() 满足一个什么条件时,
满足一个什么条件时,![]() (点
(点![]() 、
、![]() 重合除外)?画出相应图形,并说明理由.(画图不写作法)
重合除外)?画出相应图形,并说明理由.(画图不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现,
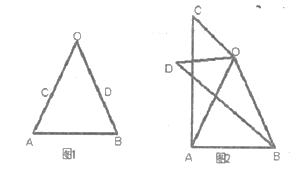
如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,将点
上一点,将点![]() 绕点
绕点![]() 顺时针旋转50°得到点
顺时针旋转50°得到点![]() ,则
,则![]() 与
与![]() 的数量关系是________________________。
的数量关系是________________________。
(2)类比探究
如图2,将(1)中的![]() 绕点
绕点![]() 在平面内旋转,(1)中的结论是否成立,并就图2的情形说明理由。
在平面内旋转,(1)中的结论是否成立,并就图2的情形说明理由。
(3)拓展延伸
![]() 绕点
绕点![]() 在平面旋转,当旋转到
在平面旋转,当旋转到![]() 时,请直接写出
时,请直接写出![]() 度数。
度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
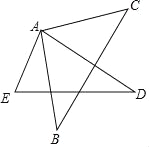
【题目】将一副三角板的两个直角顶点叠放在一起拼成如下的图形.若∠EAB=40°,则∠CAD=____;将△ABC绕直角顶点A旋转时,保持AD在∠BAC的内部,设∠EAC=x°,∠BAD=y°,则x与y的关系是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知命题“等腰三角形两腰上的高线长相等”
(1)请写出该命题的逆命题;
(2)判断(1)中命题的真假,并画出图形,补充已知,求证,及证明过程.
图形:
已知:在△ABC中,CD⊥AB,BE⊥AC,且______.
求证:______.
证明:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com