
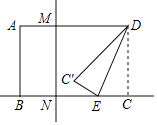
【题目】如图,在矩形ABCD中,AB=5,BC=6,点M,N分别在AD,BC上,且AM=![]() AD,BN=
AD,BN=![]() BC,E为直线BC上一动点,连接DE,将△DCE沿DE所在直线翻折得到△DC′E,当点C′恰好落在直线MN上时,CE的长为___.
BC,E为直线BC上一动点,连接DE,将△DCE沿DE所在直线翻折得到△DC′E,当点C′恰好落在直线MN上时,CE的长为___.
【答案】![]() 或10.
或10.
【解析】
由矩形的性质得到DC=AB=5,∠A=90°,AD=BC=6,根据已知条件得到AM=BN,推出四边形ABNM的矩形,得到∠NMA=∠NMD=90°,MN=AB=5,根据折叠的性质得到DC′=DC=5,C′E=CE,根据勾股定理得到C′M=![]() ,根据矩形的判定和性质得到CN=DM=4,∠CNM=90°,再由勾股定理即可得到结论.
,根据矩形的判定和性质得到CN=DM=4,∠CNM=90°,再由勾股定理即可得到结论.
解:∵四边形ABCD是矩形,
∴DC=AB=5,∠A=90°,AD=BC=6,
∵AM=![]() AD=2,BN=
AD=2,BN=![]() BC=2,
BC=2,
∴AM=BN,
∵AM∥BN,
∴四边形ABNM的矩形,
∴∠NMA=∠NMD=90°,MN=AB=5,
∵将△DCE沿DE所在直线翻折得到△DC′E,
∴DC′=DC=5,C′E=CE,
∵AM=2,
∴DM=AD﹣AM=6﹣2=4,
如图1,
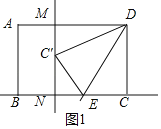
在Rt△C′MD中,C′M=![]() ,
,
∴C′N=MN﹣C′M=5﹣3=2,
∵∠CDM=∠DCN=∠NMD=90°,
∴四边形CDMN是矩形,
∴CN=DM=4,∠CNM=90°,
NE=CN﹣CE=4﹣CE,
在Rt△C′NE中,∵NE2+C′N2=C′E2,
∴(4﹣CE)2+22=CE2,
解得:CE=![]() .
.
如图2,
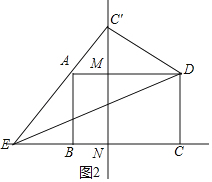
在Rt△C′MD中,C′M=![]() ,
,
∴C′N=MN+C′M=5+3=8,
∵∠CDM=∠DCN=∠NMD=90°,
∴四边形CDMN是矩形,
∴CN=DM=4,∠CNM=∠MNE=90°,
NE=CE﹣CN=CE﹣4,
在Rt△C′NE中,∵NE2+C′N2=C′E2,
∴(CE﹣4)2+82=CE2,
解答:CE=10,
故答案为:![]() 或10.
或10.


科目:初中数学 来源: 题型:
【题目】如图,在一面靠墙的空地上用长24m的篱笆,围成中间隔有两道篱笆的长方形花圃,设花圃的一边AB为x(m),面积S(m2).

(1)求S与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)若墙的最大可用长度为8m,求围成花圃的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D测得塔顶的仰角为30°.
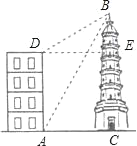
求:(1)∠DBA的度数;(2)塔高BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,对角线AC,BD相交于点O.
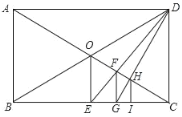
(1)过点O作OE⊥BC于点E,连接DE交OC于点F,作FG⊥BC于G点,则△ABC与△FGC是位似图形吗?若是,请说出位似中心,并求出位似比;若不是,请说明理由.
(2)连接DG交AC于点H,作HI⊥BC于I,试确定![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
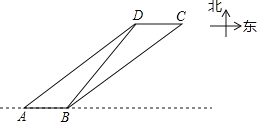
【题目】如图为某海域示意图,其中灯塔D的正东方向有一岛屿C.一艘快艇以每小时20nmile的速度向正东方向航行,到达A处时得灯塔D在东北方向上,继续航行0.3h,到达B处时测得灯塔D在北偏东30°方向上,同时测得岛屿C恰好在B处的东北方向上,此时快艇与岛屿C的距离是多少?(结果精确到1nmile.参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正五边形ABCDE,AF∥CD交DB的延长线于点F,交DE的延长线于点G.
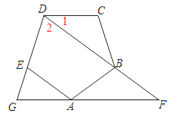
(1)写出图中所有的等腰三角形;
(2)求证:∠G=2∠F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(9,0).直线y=kx-3恰好平分⊙P的面积,那么k的值是 ( )

A. ![]()
B. ![]()
C. ![]()
D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com