
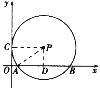
【题目】如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(9,0).直线y=kx-3恰好平分⊙P的面积,那么k的值是 ( )

A. ![]()
B. ![]()
C. ![]()
D. 2
【答案】A
【解析】
连接PC,PA,过点P作PD⊥AB于点D,根据切线的性质可知PC⊥y轴,故可得出四边形PDOC是矩形,所以PD=OC=3,再求出AB的长,由垂径定理可得出AD的长,故可得出OD的长,进而得出P点坐标,再把P点坐标代入直线y=kx-3即可得出结论.
连接PC,PA,过点P作PD⊥AB于点D,∵⊙P与y轴相切于点C(0,3),∴PC⊥y轴,∴四边形PDOC是矩形,∴PD=OC=3,∵A(1,0),B(9,0),∴AB=9-1=8,∴AD=![]() AB=
AB=![]() ×8=4,∴OD=AD+OA=4+1=5,∴P(5,3),∵直线y=kx-3恰好平分⊙P的面积,∴点P在直线y=kx-3上,∴3=5k-3,解得
×8=4,∴OD=AD+OA=4+1=5,∴P(5,3),∵直线y=kx-3恰好平分⊙P的面积,∴点P在直线y=kx-3上,∴3=5k-3,解得![]() .故选A.
.故选A.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
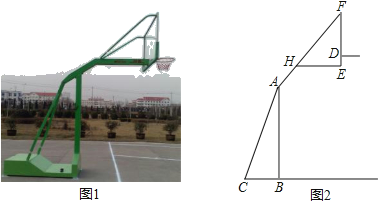
【题目】如图1,2分别是某款篮球架的实物图与示意图,AB⊥BC于点B,底座BC=1.3米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC.EF⊥EH于点E,已知AH=![]() 米,HF=
米,HF=![]() 米,HE=1米.
米,HE=1米.
(1)求篮板底部支架HE与支架AF所成的∠FHE的度数.
(2)求篮板底部点E到地面的距离,(精确到0.01米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
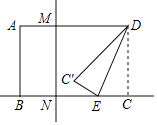
【题目】如图,在矩形ABCD中,AB=5,BC=6,点M,N分别在AD,BC上,且AM=![]() AD,BN=
AD,BN=![]() BC,E为直线BC上一动点,连接DE,将△DCE沿DE所在直线翻折得到△DC′E,当点C′恰好落在直线MN上时,CE的长为___.
BC,E为直线BC上一动点,连接DE,将△DCE沿DE所在直线翻折得到△DC′E,当点C′恰好落在直线MN上时,CE的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠BAD=120°,点E在射线AC上(不包括点A和点C),过点E的直线GH交直线AD于点G,交直线BC于点H,且GH∥DC,点F在BC的延长线上,CF=AG,连接ED,EF,DF.
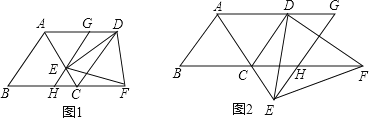
(1)如图1,当点E在线段AC上时,
①判断△AEG的形状,并说明理由.
②求证:△DEF是等边三角形.
(2)如图2,当点E在AC的延长线上时,△DEF是等边三角形吗?如果是,请证明你的结论;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心,则∠AIB的度数是( )
A. 120°B. 125°C. 135°D. 150°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com