
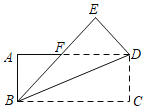
【题目】如图,四边形ABCD是矩形纸片,将△BCD沿BD折叠,得到△BED,BE交AD于点F,AB=3.AF:FD=1:2,则AF=_____.
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】数轴上的A、B、C三点所表示的数分别为a、b、1,且|a﹣1|+|b﹣1|=|a﹣b|,则下列选项中,满足A、B、C三点位置关系的数轴为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七年级学生体育测试情况,在七年级各班随机抽取了部分学生的体育测试成绩,按![]() 四个等级进行统计(说明:
四个等级进行统计(说明:![]() 级:90分~100分;
级:90分~100分;![]() 级:75分~89分;
级:75分~89分;![]() 级:60分~74分;
级:60分~74分;![]() 级:60分以下),并将统计结果绘制成两个不完整的统计图,请你结合统计图中所给信息解答下列问题:
级:60分以下),并将统计结果绘制成两个不完整的统计图,请你结合统计图中所给信息解答下列问题:
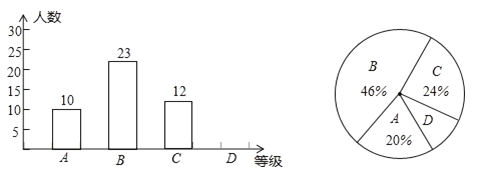
(1)学校在七年级各班共随机调查了________名学生;
(2)在扇形统计图中,![]() 级所在的扇形圆心角的度数是_________;
级所在的扇形圆心角的度数是_________;
(3)请把条形统计图补充完整;
(4)若该校七年级有500名学生,请根据统计结果估计全校七年级体育测试中![]() 级学生约有多少名?
级学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 5 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
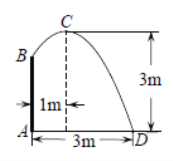
【题目】如图,在喷水池的中心![]() 处竖直安装一根水管
处竖直安装一根水管![]() ,水管的顶端安有一个喷水头,使喷出的抛物线形水柱在与池中心
,水管的顶端安有一个喷水头,使喷出的抛物线形水柱在与池中心![]() 的水平距离为1m处达到最高点
的水平距离为1m处达到最高点![]() ,高度为3m,水柱落地点
,高度为3m,水柱落地点![]() 离池中心
离池中心![]() 处3m,以水平方向为
处3m,以水平方向为![]() 轴,建立平面直角坐标系,若选取点
轴,建立平面直角坐标系,若选取点![]() 为坐标原点时的抛物线的表达式为
为坐标原点时的抛物线的表达式为![]() ,则选取点
,则选取点![]() 为坐标原点时的抛物线表达式为______,其中自变量的取值范围是______,水管
为坐标原点时的抛物线表达式为______,其中自变量的取值范围是______,水管![]() 的长为______m.
的长为______m.
查看答案和解析>>
科目:初中数学 来源: 题型:
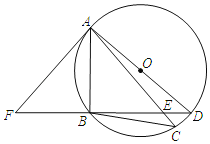
【题目】如图,AD是⊙O的直径,弧BA=弧BC,BD交AC于点E,点F在DB的延长线上,且∠BAF=∠C.
(1)求证:AF是⊙O的切线;
(2)求证:△ABE∽△DBA;
(3)若BD=8,BE=6,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 的切线,
的切线,![]() 为弦,连接
为弦,连接![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,且
,且![]() .
.
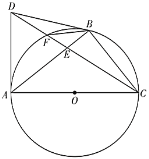
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
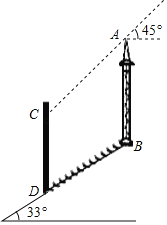
【题目】如图,在坡角为33°的山坡上有一建筑物AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得建筑物AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求建筑物AB的高(AB,CD均与水平面垂直,参考数据:sin33°=0.54,cos33°=0.84,tan33°=0.65)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com