
【题目】如图,在坡角为33°的山坡上有一建筑物AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得建筑物AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求建筑物AB的高(AB,CD均与水平面垂直,参考数据:sin33°=0.54,cos33°=0.84,tan33°=0.65)
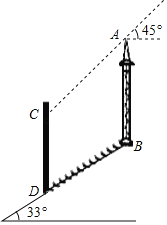
【答案】建筑物AB的高约为5.8m.
【解析】
过点C作CE⊥AB于E,过点B作BF⊥CD于F,根据正弦的定义求出DF,根据余弦的定义求出BF,根据矩形的性质、结合图形计算,得到答案.
解:过点C作CE⊥AB于E,过点B作BF⊥CD于F,
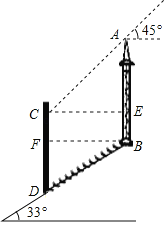
在Rt△BFD中,sin∠DBF=![]() ,
,
则DF=BDsin∠DBF≈6×0.54=3.24,
cos∠DBF=![]() ,
,
则BF=BDcos∠DBF≈6×0.84=5.04,
∵AB∥CD,CE⊥AB,BF⊥CD,
∴四边形BFCE为矩形,
∴BF=CE=5.04,CF=BE=CD﹣DF=4﹣3.24=0.76,
在Rt△ACE中,∠ACE=45°,
∴AE=CE=5.04,
∴AB=AE+BE=5.04+0.76=5.8,
答:建筑物AB的高约为5.8m.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°.
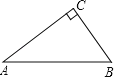
(1)以AB边上一点O为圆心作⊙O,使⊙O经过点A,C;(保留作图痕迹,不写作法)
(2)判断点B与⊙O的位置关系是 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
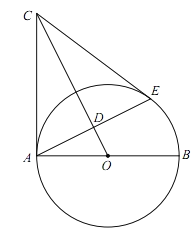
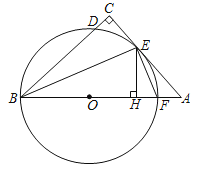
【题目】已知:如图,AB是⊙O的直径,点C是过点A的⊙O的切线上一点,连接OC,过点A作OC的垂线交OC于点D,交⊙O于点E,连接CE.
(1)求证:CE与⊙O相切;
(2)连结BD并延长交AC于点F,若OA=5,sin∠BAE=![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏参加答题游戏,答对最后两道单选题就顺利通关.第一道单选题有3个选项![]() ,
,![]() ,
,![]() ,第二道单选题有4个选项
,第二道单选题有4个选项![]() ,
,![]() ,
,![]() ,
,![]() ,这两道题小敏都不会,不过小敏还有一个“求助”机会,使用“求助”可以去掉其中一道题的一个错误选项.假设第一道题的正确选项是
,这两道题小敏都不会,不过小敏还有一个“求助”机会,使用“求助”可以去掉其中一道题的一个错误选项.假设第一道题的正确选项是![]() ,第二道题的正确选项是
,第二道题的正确选项是![]() ,解答下列问题:
,解答下列问题:
(1)如果小敏第一道题不使用“求助”,那么她答对第一道题的概率是________;
(2)如果小敏将“求助”留在第二道题使用,用画树状图或列表的方法,求小敏顺利通关的概率;
(3)小敏选第________道题(选“一”或“二”)使用“求助”,顺利通关的可能性更大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小鲁在一个不透明的盒子里装了5个除颜色外其他都相同的小球,其中有3个是红球,2个是绿球,每次拿一个球然后放回去,拿2次,则至少有一次取到绿球的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,若CD=1,EH=3,求BE长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com