
����Ŀ����ͼ���ı���ABCD�����Σ���BAD��120������E������AC�ϣ���������A�͵�C��������E��ֱ��GH��ֱ��AD�ڵ�G����ֱ��BC�ڵ�H����GH��DC����F��BC���ӳ����ϣ�CF��AG������ED��EF��DF��
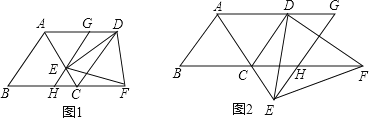
��1����ͼ1������E���߶�AC��ʱ��
���ж���AEG����״����˵�����ɣ�
����֤����DEF�ǵȱ������Σ�
��2����ͼ2������E��AC���ӳ�����ʱ����DEF�ǵȱ�������������ǣ���֤����Ľ��ۣ�������ǣ���˵�����ɣ�
���𰸡���1������AEG�ǵȱ������Σ����ɼ���������֤������������2����DEF�ǵȱ������Σ����ɼ�������
��������
��1���������ε����ʵó�AD��BC��AB��BC��CD��AD��AB��CD����CAD��![]() ��BAD��60������ƽ���ߵ����ʵó���BAD����ADC��180������ADC��60������AGE����ADC��60�����ó���AGE����EAG����AEG��60�������ɵó���AEG�ǵȱ������Σ�
��BAD��60������ƽ���ߵ����ʵó���BAD����ADC��180������ADC��60������AGE����ADC��60�����ó���AGE����EAG����AEG��60�������ɵó���AEG�ǵȱ������Σ�
���ɵȱ������ε����ʵó�AG��AE������֪�ó�AE��CF�������ε����ʵó���BCD����BAD��120�����ó���DCF��60������CAD��֤����AED�ա�CFD��SAS�����ó�DE��DF����ADE����CDF����֤����EDF��60�������ɵó���DEF�ǵȱ������Σ�
��2��ͬ��1���ٵã���AEG�ǵȱ������Σ��ó�AG��AE������֪�ó�AE��CF�������ε����ʵó���BCD����BAD��120������CAD��![]() ��BAD��60�����ó���FCD��60������CAD��֤����AED�ա�CFD��SAS�����ó�DE��DF����ADE����CDF����֤����EDF��60�������ɵó���DEF�ǵȱ������Σ�
��BAD��60�����ó���FCD��60������CAD��֤����AED�ա�CFD��SAS�����ó�DE��DF����ADE����CDF����֤����EDF��60�������ɵó���DEF�ǵȱ������Σ�
��1�����⣺��AEG�ǵȱ������Σ��������£�
���ı���ABCD�����Σ���BAD��120����
��AD��BC��AB��BC��CD��AD��AB��CD����CAD��![]() ��BAD��60����
��BAD��60����
���BAD+��ADC��180����
���ADC��60����
��GH��DC��
���AGE����ADC��60����
���AGE����EAG����AEG��60����
���AEG�ǵȱ������Σ�
��֤�����ߡ�AEG�ǵȱ������Σ�
��AG��AE��
��CF��AG��
��AE��CF��
���ı���ABCD�����Σ�
���BCD����BAD��120����
���DCF��60������CAD��
����AED����CFD�� ��
��
���AED�ա�CFD��SAS��
��DE��DF����ADE����CDF��
�ߡ�ADC����ADE+��CDE��60����
���CDF+��CDE��60����
����EDF��60����
���DEF�ǵȱ������Σ�
��2���⣺��DEF�ǵȱ������Σ��������£�
ͬ��1�����ã���AEG�ǵȱ������Σ�
��AG��AE��
��CF��AG��
��AE��CF��
���ı���ABCD�����Σ�
���BCD����BAD��120������CAD��![]() ��BAD��60����
��BAD��60����
���FCD��60������CAD��
����AED����CFD�� ��
��
���AED�ա�CFD��SAS����
��DE��DF����ADE����CDF��
�ߡ�ADC����ADE����CDE��60����
���CDF����CDE��60����
����EDF��60����
���DEF�ǵȱ������Σ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����㣺 ![]()
��2����֪����ͼ���ڡ�ABC�У�AB��AC����D��E��F�ֱ��ǡ�ABC���ߵ��е㣬��֤���ı���AEDF�����Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��
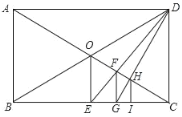
��1������O��OE��BC�ڵ�E������DE��OC�ڵ�F����FG��BC��G�㣬����ABC����FGC��λ��ͼ�������ǣ���˵��λ�����ģ������λ�Ʊȣ������ǣ���˵�����ɣ�
��2������DG��AC�ڵ�H����HI��BC��I����ȷ��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�������ABCDE��AF��CD��DB���ӳ����ڵ�F����DE���ӳ����ڵ�G��
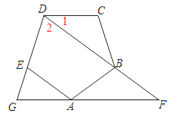
��1��д��ͼ�����еĵ��������Σ�
��2����֤����G=2��F��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ž��õĿ��ٷ�չ����������Խ��Խ�ܵ����ǵĹ�ע��ijУѧ����Ϊ���˽���������֪ʶ���ռ��������������˲���ѧ������������Ϊ���dz��˽������˽������˽�����������˽������࣬�������������Ƴ���������ͳ��ͼ��

��1�����α������ѧ���ж���������ȫ����ͳ��ͼ��
��2�����Ƹ�У1200��ѧ�������dz��˽��������˽������������Ƕ��٣�
��3������������dz��˽�����ѧ������2������������ΪŮ�������������ȡ2����ȫУ����������֪ʶ�����������û���״ͼ���б��ķ�������ǡ�ó鵽һ��һŮ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P��y�������ڵ�C(0��3)����x���ཻ�ڵ�A(1��0)��B(9��0).ֱ��y=kx-3ǡ��ƽ�֡�P���������ôk��ֵ�� ( )

A. ![]()
B. ![]()
C. ![]()
D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC��б��AB��y���ϣ���AC��x�ύ�ڵ�D������A��D�����Բ��Բ��Fǡ����y���ϣ���F���BC�����ڵ�E����x�ύ�ڵ�M����y���ཻ����һ��G������AE��
��1����֤��AEƽ�֡�BAC��
��2������A��D������ֱ�Ϊ��0����1������2��0��������F�İ뾶��
��3��������M��F��D�������ߵĽ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
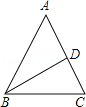
����Ŀ����ͼ������ABC�У�AB=AC��![]() ��BD����ABC���ܳ���Ϊ30cm��15cm�����֣���AB�ij�Ϊ________��
��BD����ABC���ܳ���Ϊ30cm��15cm�����֣���AB�ij�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ����
����![]() ��
��![]() ������Ӱ
������Ӱ![]() ���ٹ�
���ٹ�![]() ��
��![]() ����
����![]() ��
��![]() ������Ӱ
������Ӱ![]() ���������ȥ����²������õ���������Ӱ�����ε����֮��Ϊ�� ��
���������ȥ����²������õ���������Ӱ�����ε����֮��Ϊ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com