
【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,经过A,D两点的圆的圆心F恰好在y轴上,⊙F与边BC相切于点E,与x轴交于点M,与y轴相交于另一点G,连接AE.
(1)求证:AE平分∠BAC;
(2)若点A,D的坐标分别为(0,﹣1),(2,0),求⊙F的半径;
(3)求经过三点M,F,D的抛物线的解析式.

【答案】(1)详见解析;(2)⊙F的半径为![]() ;(3)y=﹣
;(3)y=﹣![]() x2+
x2+![]() .
.
【解析】
(1)连接FE,先根据切线的性质知∠FEC=90°,结合∠C=90°证FE∥AC得∠EAC=∠FEA,根据FA=FE知∠FAE=∠FEA,从而得∠FAE=∠CAE,即可得证;
(2)连接FD,设⊙F的半径为r,根据FD2=(AF﹣AO)2+OD2知r2=(r﹣1)2+22,解之可得;
(3)根据圆的对称性得出点M的坐标,设抛物线的交点式,将点F坐标代入计算可得.
(1)连接FE,
∵⊙F与边BC相切于点E,
∴∠FEC=90°,
∵∠ACB=90°,
∴∠FEC+∠ACB=180°,
∴FE∥AC,
∴∠EAC=∠FEA,
∵FA=FE,
∴∠FAE=∠FEA,
∴∠FAE=∠CAE,
∴AE平分∠BAC;
(2)连接FD,
设⊙F的半径为r,
∵A(0,﹣1),D(2,0),
∴OA=1,OD=2,
在Rt△FOD中,FD2=(AF﹣AO)2+OD2,
∴r2=(r﹣1)2+22,
解得:r=![]() ,
,
∴⊙F的半径为![]() ;
;
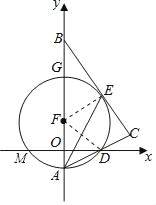
(3)∵FA=r=![]() ,OA=1,FO=
,OA=1,FO=![]() ,
,
∴F(0,![]() ),
),
∵直径AG垂直平分弦MD,点M和点D(2,0)关于y轴对称轴,
∴M(﹣2,0),
设抛物线解析式为y=a(x+2)(x﹣2),
将点F(0,![]() )代入,得:﹣4a=
)代入,得:﹣4a=![]() ,
,
解得:a=﹣![]() ,
,
则抛物线解析式为y=﹣![]() (x+2)(x﹣2)=﹣
(x+2)(x﹣2)=﹣![]() x2+
x2+![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),有下列结论:①2a+b=0,②abc>0;③方程ax2+bx+c=3有两个相等的实数根,④当y<0时,﹣2<x<4,其中正确的是( )
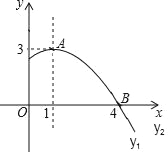
A. ②③ B. ①③ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣
(x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣![]() <0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )
<0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )
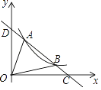
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2﹣4ax>0;②2a+b>0;③abc<0;④4a﹣2b+c<0;⑤a+b+c>0.其中正确的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )

A. 17.5° B. 12.5° C. 12° D. 10°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,测得B,C两点的俯角分别为60°和45°,已知热气球离地面的高度为120m,且大桥与地面在同一水平面上,求大桥BC的长度(结果保留整数,![]() ≈1.72).
≈1.72).
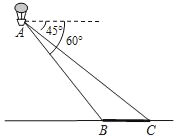
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com