
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣
(x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣![]() <0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )
<0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )
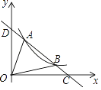
A. 4个 B. 3个 C. 2个 D. 1个
【答案】A
【解析】
根据双曲线解析式求得点A、B坐标,待定系数法可得直线解析式,即可判断①;由直线解析式求得C、D坐标,由两点间的距离公式求得AD、BC的长,即可判断②;由函数图象知直线在双曲线下方时x的范围即可判断③;利用割补法求得△AOB的面积即可判断④.
把点(m,6),B(3,n)分别代入y=![]() (x>0)得m=1,n=2,
(x>0)得m=1,n=2,
∴A点坐标为(1,6),B点坐标为(3,2),
把A(1,6),B(3,2)分别代入y=kx+b,
得![]()
![]() ,
,![]() 解得
解得![]() ,
,
∴一次函数解析式为y=2x+8,故①正确;
在y=2x+8中,当x=0时,y=8,即D(0,8),
当y=0时,2x+8=0,解得:x=4,即C(4,0),
则AD=![]() =
=![]() ,BC=
,BC=![]() =
=![]() ,
,
∴AD=BC,故②正确;
由函数图象知,直线在双曲线下方时x的范围是0<x<1或x>3,
∴kx+b6x<0的解集为0<x<1或x>3,故③正确;
分别过点A.B作AE⊥x轴,BF⊥x轴,垂足分别是E.F点.
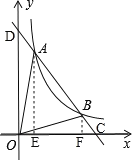
∵A(1,6),B(3,2),
∴AE=6,BF=2,
∴S△AOB=S△AOCS△BOC=![]() ×4×612×4×2=8,故④正确;
×4×612×4×2=8,故④正确;
故答案选:A.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为()cm2.
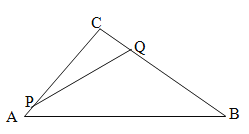
A. 19 B. 16 C. 15 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线与直线的图象如图所示,则下列说法:
①当0<x<2时, y1>y2;②y1随x的增大而增大的取值范围是x<2;③使得y2大于4的x值不存在;④若y1=2,则x=2﹣![]() 或x=1.其中正确的有( )
或x=1.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
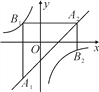
【题目】如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-![]() 上,并且满足A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2018=_______.
上,并且满足A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2018=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,经过A,D两点的圆的圆心F恰好在y轴上,⊙F与边BC相切于点E,与x轴交于点M,与y轴相交于另一点G,连接AE.
(1)求证:AE平分∠BAC;
(2)若点A,D的坐标分别为(0,﹣1),(2,0),求⊙F的半径;
(3)求经过三点M,F,D的抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
修造人 | 笔试成绩/分 | 面试成绩/分 |
甲 | 90 | 88 |
乙 | 84 | 92 |
丙 | x | 90 |
丁 | 88 | 86 |
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市教育局为了解本市中学生参加志愿者活动情况,随机拍查了某区部分八年级学生一学年来参加志愿者活动的次数,并用得到的数据绘制了如下两幅不完整的统计图.

(1)求参加这次调查统计的学生总人数及这个区八年级学生平均每人一学年来参加志愿者活动的次数;
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该区共有八年级学生![]() 人,请你估计“活动次数不少于
人,请你估计“活动次数不少于![]() 次”的学生人数大约多少人.
次”的学生人数大约多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com