
����Ŀ�����ž��õĿ��ٷ�չ����������Խ��Խ�ܵ����ǵĹ�ע��ijУѧ����Ϊ���˽���������֪ʶ���ռ��������������˲���ѧ������������Ϊ���dz��˽������˽������˽�����������˽������࣬�������������Ƴ���������ͳ��ͼ��

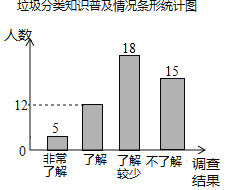
��1�����α������ѧ���ж���������ȫ����ͳ��ͼ��
��2�����Ƹ�У1200��ѧ�������dz��˽��������˽������������Ƕ��٣�
��3������������dz��˽�����ѧ������2������������ΪŮ�������������ȡ2����ȫУ����������֪ʶ�����������û���״ͼ���б��ķ�������ǡ�ó鵽һ��һŮ�ĸ��ʣ�
���𰸡���1�����α������ѧ����50�ˣ���ȫͼ�μ���������2�����Ƹ�У1200��ѧ�������dz��˽��������˽�������������408�ˣ���3��ǡ�ó鵽һ��һŮ�ĸ���Ϊ![]() ��
��
��������
��1�������˽���������������ռ�ٷֱ���������������������Զ�Ӧ�İٷֱȿ�������dz��˽��������˽���������������̶���������˽������������Ӷ���ȫͼ�Σ�
��2������������������˼�����ɵã�
��3������״ͼչʾ����20�ֵȿ��ܵĽ���������ҳ����������Ľ������Ȼ�����ø��ʹ�ʽ��⣮
��1�����α������ѧ������12��24%��50���ˣ���
�����dz��˽���������Ϊ50��10%��5���ˣ���
���˽������������Ϊ50��36%��18���ˣ���
�����˽���������Ϊ50����5+12+18����15���ˣ���
��ȫͼ�����£�
��2�����Ƹ�У1200��ѧ�������dz��˽��������˽�������������1200��![]() ��408���ˣ���
��408���ˣ���
��3������״ͼΪ��
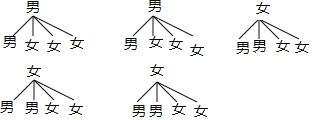
����20�ֵȿ��ܵĽ����������ǡ�ó鵽һ��һŮ����12�ֽ����
����ǡ�ó鵽һ��һŮ�ĸ���Ϊ![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2-2ax+b������C��0��-![]() ��������x�ύ�ڵ�A����B����tan
��������x�ύ�ڵ�A����B����tan![]() ACO=
ACO=![]() ��
��

��1����������ߵĽ���ʽ��
��2���������ߵĶ���ΪM����P���߶�OB��һ���㣨�����B�غϣ���![]() MPQ=45
MPQ=45![]() ������PQ���߶�BM���ڵ�Q������MPQΪ����������ʱ�����P�����꣮
������PQ���߶�BM���ڵ�Q������MPQΪ����������ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C����ABΪֱ���İ�Բ�ϣ�AB=4����CBA=30�㣬��D��AO���˶�����E���D����AC�Գƣ�DF��DE�ڵ�D������EC���ӳ����ڵ�F�����н��ۣ�

��CE=CF��
���߶�EF����СֵΪ![]() ��
��
�۵�AD=1ʱ��EF���Բ���У�
�ܵ���D�ӵ�A�˶�����Oʱ���߶�EFɨ���������4![]() ��
��
������ȷ������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȫ�ȵġ�ABC�͡�DBE��ͼ1��ʽ�ڷţ����С�ACB����DEB��90�㣬��A����D��30�㣬��E����AB�ϣ�DE����ֱ�߽�AC����ֱ����F��
��1����֤��AF��EF��DE��
��2������ͼ1�еġ�DBE�Ƶ�B˳ʱ����ת�Ǧ�����60��<��<180�㣬�����������䣬��ͼ2����ֱ��д����ʱ�߶�AF��EF��DE֮���������ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ����������д��![]() ����ʽ������a��b��Ϊ��Ȼ���������֮Ϊ����Ħ�Ŷ���������7��31��������Ħ�Ŷ�������Ϊ7��22��3��12��31��22��3��32��
����ʽ������a��b��Ϊ��Ȼ���������֮Ϊ����Ħ�Ŷ���������7��31��������Ħ�Ŷ�������Ϊ7��22��3��12��31��22��3��32��
��1����֤����28��217��������Ħ�Ŷ�����
��2����֤�����κ���������Ħ�Ŷ����ij˻�����������Ħ�Ŷ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ��ֱ������ϵ�У�����y��ax2��b��y��bx2��ax��ͼ�������(����)

A. A B. B C. C D. D
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A1��A2��A3������An��x���ϵĵ㣬��OA1��A1A2��A2A3��A3A4������An��1An��1���ֱ����A1��A2��A3������An��x��Ĵ��߽����κ���y��![]() x2(x��0)��ͼ���ڵ�P1��P2��P3������Pn.���ǡ�OA1P1�����ΪS1������P1��P1B1��A2P2�ڵ�B1���ǡ�P1B1P2�����ΪS2������P2��P2B2��A3P3�ڵ�B2���ǡ�P2B2P3�����ΪS3�������ν�����ȥ�����ǡ�Pn��1Bn��1Pn(n��1)�����ΪSn����Sn��(����)
x2(x��0)��ͼ���ڵ�P1��P2��P3������Pn.���ǡ�OA1P1�����ΪS1������P1��P1B1��A2P2�ڵ�B1���ǡ�P1B1P2�����ΪS2������P2��P2B2��A3P3�ڵ�B2���ǡ�P2B2P3�����ΪS3�������ν�����ȥ�����ǡ�Pn��1Bn��1Pn(n��1)�����ΪSn����Sn��(����)

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,ֱ��l�Ǿ���ABCD��һ���Գ���,AD=2AB,��P��ֱ��l��һ��,��ʹ����PAB����PBC��Ϊ����������,�����������ĵ�P����( )��.

A.1B.2C.3D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ�̣�1����2x2��4x��5��0.����ʽ���� (2) x2��4x��1��0.���䷽����
��3��(y��1)2��2y(1��y)��0.����ʽ�ֽⷨ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com