
【题目】解方程(1):2x2-4x-5=0.(公式法) (2) x2-4x+1=0.(配方法)
(3)(y-1)2+2y(1-y)=0.(因式分解法)
【答案】(1)x=![]() ;(2)x=
;(2)x=![]() ; (3)y=
; (3)y=![]()
【解析】分析: (1)先找a,b,c,再求△,根据根的判别式判断方程根的情况,再代入公式计算即可;
(2)先移项,再方程两边同加上一次项系数一般半的平方,再直接开平方即可;
(3)先变形,再提公因式,得出两个一元一次方程求解即可.
详解:
(1):2x2-4x-5=0.
∵a=2,b=4,c=5,
b4ac=(4) 4×2×(5)=56>0.
∴x=![]() =
=![]() .
.
∴x=![]() ,x=
,x=![]() .
.
(2) x2-4x+1=0.
x4x+4=41,即(x2) =3.
∴x=2+![]() ,x=2
,x=2![]() .
.
(3)∵(y1) +2y(1y)=0,
∴(y1) 2y(y1)=0.
∴(y1)(y12y)=0.
∴y1=0或y12y=0.
∴y=1,y=1.
点睛: 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法和公式法解一元二次方程.


科目:初中数学 来源: 题型:
【题目】(本题12分)如图1,在平面直角坐标系中,四边形OABC各顶点的坐标分别O(0,0),A(3, ![]() ),B(9,5
),B(9,5 ![]() ),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3,
),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OAABBC运动,在OA,AB,BC上运动的速度分别为3, ![]() ,
, ![]() (单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.
(单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.
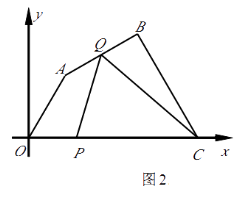
(1)求AB所在直线的函数表达式.
(2)如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值.
(3)在P,Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的括号内
![]() , -
, -![]() , 0,
, 0, ![]() ,‐3.1415926, 20%, ‐3
,‐3.1415926, 20%, ‐3![]() , 2, -1,3.1010010001…(每两个1之间逐次增加1个0)
, 2, -1,3.1010010001…(每两个1之间逐次增加1个0)
①正数集合{ ……}
②负数集合{ ……}
③整数集合{ ……}
④负分数集合{ ……}
⑤无理数集合{ ……}
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是( )

A. 12厘米 B. 16厘米 C. 20厘米 D. 28厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为6,则k的值为 .
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为6,则k的值为 . 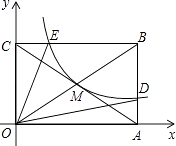
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将四根长度相等的细木条首尾相接钉成四边形ABCD,当∠B=90°时,测得AC=4,改变它的形状使∠B=60°,此时AC的长度为( ) 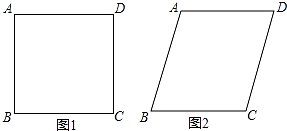
A.![]()
B.2
C.![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:有理数xA用数轴上点A表示,xA叫做点A在数轴上的坐标;有理数xB用数轴上点B表示,xB叫做点B在数轴上的坐标.|AB|表示数轴上的两点A,B之间的距离.
(1)借助数轴,完成下表:
xA | xB | xA﹣xB | |AB| |
3 | 2 | 1 | 1 |
1 | 5 |
|
|
2 | ﹣3 |
|
|
﹣4 | 1 |
|
|
﹣5 | ﹣2 |
|
|
﹣3 | ﹣6 |
|
|
(2)观察(1)中的表格内容,猜想|AB|= ;(用含xA,xB的式子表示,不用说理)
(3)已知点A在数轴上的坐标是﹣2,且|AB|=8,利用(2)中的结论求点B在数轴上的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com