
【题目】如图,已知正五边形ABCDE,AF∥CD交DB的延长线于点F,交DE的延长线于点G.
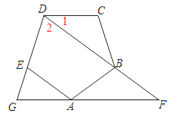
(1)写出图中所有的等腰三角形;
(2)求证:∠G=2∠F.
【答案】(1)等腰三角形有:△BCD,△ABF,△FDG,△AEG;(2)见解析.
【解析】
(1)利用等腰三角形的性质以及正五边形的性质得出各角度进而得出答案;
(2)分别得出:∠G与∠F的度数进而得出它们之间的关系.
(1)解:∵DC=BC,
∴△CDB是等腰三角形,
∵∠C=108°,
∴∠1=∠CBD=36°,
∵AF∥CD,
∴∠F=∠1=36°,
可得四边形DEAB是等腰梯形,
∴∠DBA=∠2=72°,
∴∠F=∠BAF=36°,
∴△BAF是等腰三角形,
进而可得:∠GEA=∠G=∠2=72°,
∴△FDG,△AEG是等腰三角形,
故等腰三角形有:△BCD,△ABF,△FDG,△AEG.
(2)证明:∵五边形ABCDE是正五边形,
∴∠C=∠CDE=108°,CD=CB.
得∠1=36°,
∴∠2=108°﹣36°=72°.
又∵AF∥CD,
∴∠F=∠1=36°,
故∠G=180°﹣∠2﹣∠F=180°﹣72°﹣36°=72°=2∠F.


科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程![]() 是关于x的一元二次方程.
是关于x的一元二次方程.
(1)判断方程![]() 的根的情况为 (填序号);
的根的情况为 (填序号);
①方程有两个相等的实数根; ②方程有两个不相等的实数根;
③方程无实数根; ④无法判断
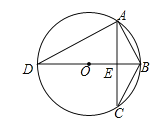
(2)如图,若△ABC内接于半径为2的⊙O,直径BD⊥AC于点E,且∠DAC=60°,求方程![]() 的根;
的根;
(3)若![]() 是方程
是方程![]() 的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.
的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M,N是以AB为直径的⊙O上的点,且![]() =
=![]() ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
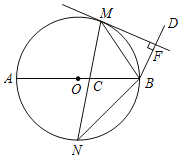
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
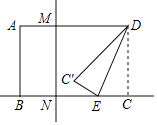
【题目】如图,在矩形ABCD中,AB=5,BC=6,点M,N分别在AD,BC上,且AM=![]() AD,BN=
AD,BN=![]() BC,E为直线BC上一动点,连接DE,将△DCE沿DE所在直线翻折得到△DC′E,当点C′恰好落在直线MN上时,CE的长为___.
BC,E为直线BC上一动点,连接DE,将△DCE沿DE所在直线翻折得到△DC′E,当点C′恰好落在直线MN上时,CE的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品的进价为每件30元,销售过程中发现月销售量y(件)与销售单价x(元)之间的关系如图所示.
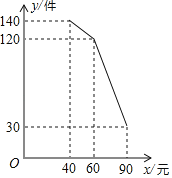
(1)根据图象直接写出y与x之间的函数关系式.
(2)设这种商品月利润为W(元),求W与x之间的函数关系式.
(3)这种商品的销售单价定为多少元时,月利润最大?最大月利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠BAD=120°,点E在射线AC上(不包括点A和点C),过点E的直线GH交直线AD于点G,交直线BC于点H,且GH∥DC,点F在BC的延长线上,CF=AG,连接ED,EF,DF.
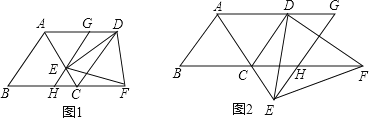
(1)如图1,当点E在线段AC上时,
①判断△AEG的形状,并说明理由.
②求证:△DEF是等边三角形.
(2)如图2,当点E在AC的延长线上时,△DEF是等边三角形吗?如果是,请证明你的结论;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+bx+c与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点A的坐标为(﹣4,0),B的坐标为(1,0),且OC=4OB.
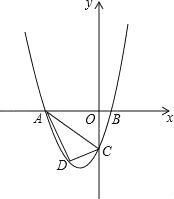
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求三角形ACD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com