
【题目】已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程![]() 是关于x的一元二次方程.
是关于x的一元二次方程.
(1)判断方程![]() 的根的情况为 (填序号);
的根的情况为 (填序号);
①方程有两个相等的实数根; ②方程有两个不相等的实数根;
③方程无实数根; ④无法判断
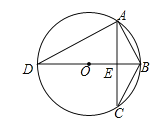
(2)如图,若△ABC内接于半径为2的⊙O,直径BD⊥AC于点E,且∠DAC=60°,求方程![]() 的根;
的根;
(3)若![]() 是方程
是方程![]() 的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.
的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.
【答案】(1)②;(2)![]() ,
,![]() ;(3)a=2,b=3,c=2
;(3)a=2,b=3,c=2
【解析】
(1)先计算判别式的值得到△=b2+4ac,由于a、b、c为三角形的边长,则△>0,然后根据判别式的意义判断方程根的情况;
(2)连接OA,如图,根据垂径定理,由BD⊥AC得到,弧AB=弧CB,弧AD=弧CD,再利用圆心角、弧、弦的关系得到AB=CB,利用圆周角定理得到∠ABD=∠DAC=60°,则可判断△OAB为等边三角形,得到AB=OB=2,AE=![]() OB=
OB=![]() ,所以AC=2AE=2
,所以AC=2AE=2![]() ,即a=2,b=2
,即a=2,b=2![]() ,c-2,然后利用求根公式法解方程2x2+2
,c-2,然后利用求根公式法解方程2x2+2![]() x-2=0;
x-2=0;
(3)根据一元二次方程根的定义,把![]() 代入ax2+bx-c=0后变形得到
代入ax2+bx-c=0后变形得到![]() ,易得b<4,利用a、b、c的长均为整数得到b=1,2,3,然后分类讨论:当b=1时,ac=12,;当b=2时,ac=8;当b=3时,ac=4,再利用整数的整除性求出a、c的值,然后利用三角形三边的关系确定满足条件的a、b、c的值.
,易得b<4,利用a、b、c的长均为整数得到b=1,2,3,然后分类讨论:当b=1时,ac=12,;当b=2时,ac=8;当b=3时,ac=4,再利用整数的整除性求出a、c的值,然后利用三角形三边的关系确定满足条件的a、b、c的值.
(1)△=b2-4a(-c)=b+4ac,
∵a、b、c分别为∠A、∠B、∠C的对边,即a、b、c都是正数,
∴△>0,
∴方程有两个不相等的实数根;
故选②;
(2)连接OA,如图,
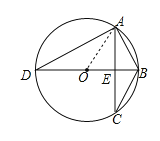
∵BD⊥AC,
∴弧AB=弧CB,弧AD=弧CD,
∴AB=CB,∠ABD=∠DAC=60°,
∴△OAB为等边三角形,
∴AB=OB=2,
∴AE=![]() OB=
OB=![]()
∴AC=2AE=![]() ,
,
即a=2,b=![]() ,c=2,
,c=2,
方程![]() 变形为
变形为![]() ,
,
整理得:,
解得![]() ,
,![]() ;
;
(3)把![]() 代入
代入![]() 得:
得:![]()
整理得:![]() ,则4-b>0,
,则4-b>0,
即b<4,
∵a、b、c的长均为整数,
∴b=1,2,3,
当b=1时,ac=12,则a=1,c=12;a=2,c=6;a=3,c=4;a=6,c=2;a=12,c=1,都不符合三角形三边的关系,舍去;
当b=2时,ac=8,则a=1,c=8;a=2,c=4;a=4,c=2;a=8,c=1,都不符合三角形三边的关系,舍去;
当b=3时,ac=4,则a=1,c=4;a=2,c=2;a=4,c=1,其中a=2,c=2符合三角形三边的关系,
∴a=2,b=3,c=2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
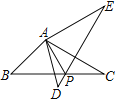
【题目】问题背景:如图,将![]() 绕点
绕点![]() 逆时针旋转60°得到
逆时针旋转60°得到![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,可推出结论:
,可推出结论:![]()
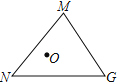
问题解决:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 是
是![]() 内一点,则点
内一点,则点![]() 到
到![]() 三个顶点的距离和的最小值是___________
三个顶点的距离和的最小值是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴正半轴相交,其顶点坐标为
轴正半轴相交,其顶点坐标为![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④方程
;④方程![]() 有两个相等的实数根,其中正确的结论是________.(只填序号即可).
有两个相等的实数根,其中正确的结论是________.(只填序号即可).
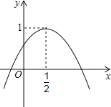
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一面靠墙的空地上用长24m的篱笆,围成中间隔有两道篱笆的长方形花圃,设花圃的一边AB为x(m),面积S(m2).

(1)求S与x之间的函数关系式,并直接写出自变量x的取值范围;
(2)若墙的最大可用长度为8m,求围成花圃的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
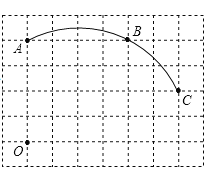
(1)请完成如下操作:
①以点O为坐标原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系; ②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD.
(2)请在(1)的基础上,完成下列填空:
①写出点的坐标:C 、D ;
②⊙D的半径= (结果保留根号);
③若E(7,0),试判断直线EC与⊙D的位置关系,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
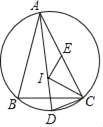
【题目】点I为△ABC的内心,连AI交△ABC的外接圆于点D,若AI=2CD,点E为弦AC的中点,连接EI,IC,若IC=6,ID=5,则IE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D测得塔顶的仰角为30°.
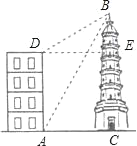
求:(1)∠DBA的度数;(2)塔高BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正五边形ABCDE,AF∥CD交DB的延长线于点F,交DE的延长线于点G.
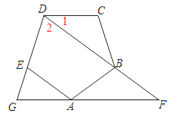
(1)写出图中所有的等腰三角形;
(2)求证:∠G=2∠F.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com