
【题目】如图,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D测得塔顶的仰角为30°.
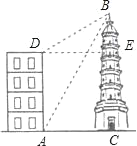
求:(1)∠DBA的度数;(2)塔高BC.
【答案】(1)∠DBA=30°;(2)塔高BC的高为45m.
【解析】
(1)根据题意得:AD∥BC,∠BDE=30°,∠BAC=60°,∠BCA=90°,即可求得∠DBA的度数;
(2)在Rt△BDE中与Rt△ABC中,利用三角函数的正切即可得BE=DEtan∠BDE=DEtan30°=![]() DE,BC=ACtan∠BAC=ACtan60°=
DE,BC=ACtan∠BAC=ACtan60°=![]() AC,然后设BC=xm,即可求得BC的长.
AC,然后设BC=xm,即可求得BC的长.
解:(1)根据题意得:AD∥BC,∠BDE=30°,∠BAC=60°,∠BCA=90°,
∴∠ABC=90°﹣∠BAC=30°,
∴∠DBA=∠ABC=30°;
(2)在Rt△BDE中,BE=DEtan∠BDE=DEtan30°=![]() DE,
DE,
在Rt△ABC中,BC=ACtan∠BAC=ACtan60°=![]() AC,
AC,
∵AC=DE,
∴![]() BE=
BE=![]() BC,
BC,
设BC=xm,
∴![]() (x﹣30)=
(x﹣30)=![]() x,
x,
解得:x=45,
∴塔高BC的高为45m.


科目:初中数学 来源: 题型:
【题目】春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
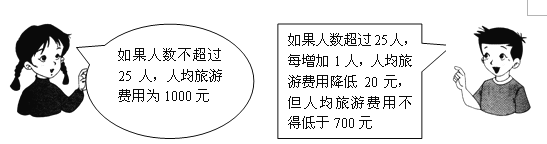 某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
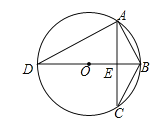
【题目】已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程![]() 是关于x的一元二次方程.
是关于x的一元二次方程.
(1)判断方程![]() 的根的情况为 (填序号);
的根的情况为 (填序号);
①方程有两个相等的实数根; ②方程有两个不相等的实数根;
③方程无实数根; ④无法判断
(2)如图,若△ABC内接于半径为2的⊙O,直径BD⊥AC于点E,且∠DAC=60°,求方程![]() 的根;
的根;
(3)若![]() 是方程
是方程![]() 的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.
的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,AB⊥BC于点B,底座BC=1.3米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC.EF⊥EH于点E,已知AH=![]() 米,HF=
米,HF=![]() 米,HE=1米.
米,HE=1米.
(1)求篮板底部支架HE与支架AF所成的∠FHE的度数.
(2)求篮板底部点E到地面的距离,(精确到0.01米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
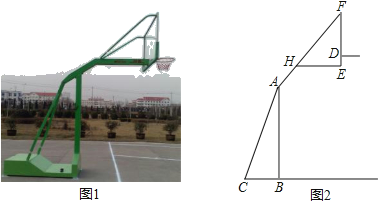
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图(1)所示,成本y2与销售月份之间的关系如图(2)所示(图(1)的图象是线段图(2)的图象是抛物线)
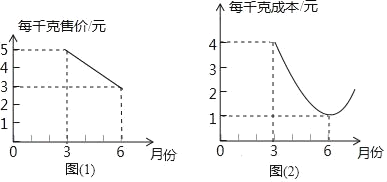
(1)分别求出y1、y2的函数关系式(不写自变量取值范围);
(2)通过计算说明:哪个月出售这种蔬菜,每千克的收益最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M,N是以AB为直径的⊙O上的点,且![]() =
=![]() ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
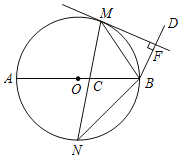
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
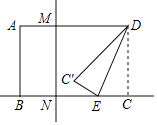
【题目】如图,在矩形ABCD中,AB=5,BC=6,点M,N分别在AD,BC上,且AM=![]() AD,BN=
AD,BN=![]() BC,E为直线BC上一动点,连接DE,将△DCE沿DE所在直线翻折得到△DC′E,当点C′恰好落在直线MN上时,CE的长为___.
BC,E为直线BC上一动点,连接DE,将△DCE沿DE所在直线翻折得到△DC′E,当点C′恰好落在直线MN上时,CE的长为___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com