
【题目】问题背景:如图,将![]() 绕点
绕点![]() 逆时针旋转60°得到
逆时针旋转60°得到![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,可推出结论:
,可推出结论:![]()
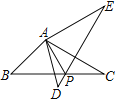
问题解决:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 是
是![]() 内一点,则点
内一点,则点![]() 到
到![]() 三个顶点的距离和的最小值是___________
三个顶点的距离和的最小值是___________
【答案】![]()
【解析】
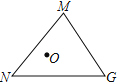
如图,将△MOG绕点M逆时针旋转60°,得到△MPQ,易知△MOP为等边三角形,继而得到点O到三顶点的距离为:ON+OM+OG=ON+OP+PQ,由此可以发现当点N、O、P、Q在同一条直线上时,有ON+OM+OG最小,此时,∠NMQ=75°+60°=135°,过Q作QA⊥NM交NM的延长线于A,利用勾股定理进行求解即可得.
如图,将△MOG绕点M逆时针旋转60°,得到△MPQ,
显然△MOP为等边三角形,
∴,OM+OG=OP+PQ,
∴点O到三顶点的距离为:ON+OM+OG=ON+OP+PQ,
∴当点N、O、P、Q在同一条直线上时,有ON+OM+OG最小,
此时,∠NMQ=75°+60°=135°,
过Q作QA⊥NM交NM的延长线于A,则∠MAQ=90°,
∴∠AMQ=180°-∠NMQ=45°,
∵MQ=MG=4![]() ,
,
∴AQ=AM=MQcos45°=4,
∴NQ=![]() ,
,
故答案为:![]() .
.



科目:初中数学 来源: 题型:
【题目】某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
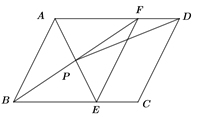
【题目】如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求PD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利44元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件。若商场平均每天要盈利1600元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经销一种商品,每件成本为20元.经市场调查发现,在一段时间内,销售量w(件)随销售单价x(元/件)的变化而变化,具体关系式为:w=-10x+500.设这种商品在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x的函数关系式;
(2)当x取何值时,利润最大?最大利润为多少元?
(3)如果物价部门规定这种商品的销售单价不得高于32元/件,公司想要在这段时间内获得2000元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
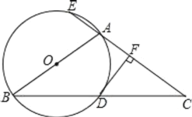
(1)证明:DF是⊙O的切线;
(2)若AC=3AE,FC=6,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1=k1x+b与反比例函数![]() 的图象交于A,B两点(点A在点B左侧),已知点A的坐标是(6,2)点B的纵坐标是﹣3.
的图象交于A,B两点(点A在点B左侧),已知点A的坐标是(6,2)点B的纵坐标是﹣3.

(1)求反比例函数和直线l1的表达式;
(2)根据图象直接写出k1x+b>![]() 的解集;
的解集;
(3)将直线l1:![]() 沿y轴向上平移后的直线l2与反比例函数
沿y轴向上平移后的直线l2与反比例函数![]() 在第一象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第一象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:
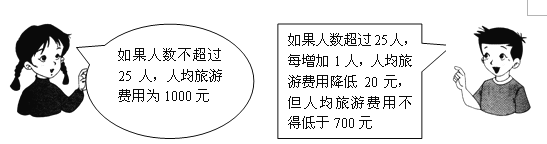 某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程![]() 是关于x的一元二次方程.
是关于x的一元二次方程.
(1)判断方程![]() 的根的情况为 (填序号);
的根的情况为 (填序号);
①方程有两个相等的实数根; ②方程有两个不相等的实数根;
③方程无实数根; ④无法判断
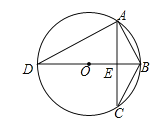
(2)如图,若△ABC内接于半径为2的⊙O,直径BD⊥AC于点E,且∠DAC=60°,求方程![]() 的根;
的根;
(3)若![]() 是方程
是方程![]() 的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.
的一个根,△ABC的三边a、b、c的长均为整数,试求a、b、c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com