
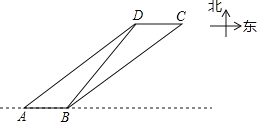
【题目】如图为某海域示意图,其中灯塔D的正东方向有一岛屿C.一艘快艇以每小时20nmile的速度向正东方向航行,到达A处时得灯塔D在东北方向上,继续航行0.3h,到达B处时测得灯塔D在北偏东30°方向上,同时测得岛屿C恰好在B处的东北方向上,此时快艇与岛屿C的距离是多少?(结果精确到1nmile.参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
【答案】此时快艇与岛屿C的距离是20nmile.
【解析】
过点D作DE⊥AB于点E,过点C作CF⊥AB于点F,由DE∥CF,DC∥EF,∠CFE=90°可得出四边形CDEF为矩形,设DE=x nmile,则AE=x (nmile),BE=![]() x(nmile),由AB=6 nmile,可得出关于x的一元一次方程,解之即可得出x的值,再在Rt△CBF中,通过解直角三角形可求出BC的长.
x(nmile),由AB=6 nmile,可得出关于x的一元一次方程,解之即可得出x的值,再在Rt△CBF中,通过解直角三角形可求出BC的长.
解:过点D作DE⊥AB于点E,过点C作CF⊥AB于点F,如图所示.

则DE∥CF,∠DEA=∠CFA=90°.
∵DC∥EF,
∴四边形CDEF为平行四边形.
又∵∠CFE=90°,
∴CDEF为矩形,
∴CF=DE.
根据题意,得:∠DAB=45°,∠DBE=60°,∠CBF=45°.
设DE=x(nmile),
在Rt△DEA中,∵tan∠DAB=![]() ,
,
∴AE=![]() =x(nmile).
=x(nmile).
在Rt△DEB中,∵tan∠DBE=![]() ,
,
∴BE=![]() =
=![]() x(nmile).
x(nmile).
∵AB=20×0.3=6(nmile),AE﹣BE=AB,
∴x﹣![]() x=6,解得:x=9+3
x=6,解得:x=9+3![]() ,
,
∴CF=DE=(9+3![]() )nmile.
)nmile.
在Rt△CBF中,sin∠CBF=![]() ,
,
∴BC=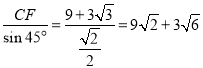 ≈20(nmile).
≈20(nmile).
答:此时快艇与岛屿C的距离是20nmile.


科目:初中数学 来源: 题型:
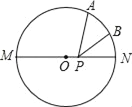
【题目】如图,MN是⊙O的直径,点A是半圆上的三等分点,点B是劣弧AN的中点,点P是直径MN上一动点.若MN=2![]() ,AB=1,则△PAB周长的最小值是( )
,AB=1,则△PAB周长的最小值是( )
A. 2![]() +1 B.
+1 B. ![]() +1 C. 2 D. 3
+1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
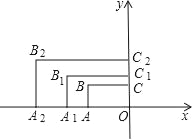
【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA,OC分别在x轴和y轴上,且OA=2.OC=1,则矩形AOCB的对称中心的坐标是___;在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的![]() 倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大
倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大![]() 倍,得到矩形A2OC2B,…,按此规律,则矩形A4OC4B4的对称中心的坐标是___.
倍,得到矩形A2OC2B,…,按此规律,则矩形A4OC4B4的对称中心的坐标是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
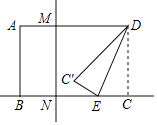
【题目】如图,在矩形ABCD中,AB=5,BC=6,点M,N分别在AD,BC上,且AM=![]() AD,BN=
AD,BN=![]() BC,E为直线BC上一动点,连接DE,将△DCE沿DE所在直线翻折得到△DC′E,当点C′恰好落在直线MN上时,CE的长为___.
BC,E为直线BC上一动点,连接DE,将△DCE沿DE所在直线翻折得到△DC′E,当点C′恰好落在直线MN上时,CE的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
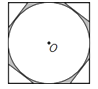
【题目】已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )
A. 32![]() ﹣32﹣4πB.
﹣32﹣4πB. ![]() C. 1D. 16﹣4π
C. 1D. 16﹣4π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC摆放在平面直角坐标系![]() 中,点A在
中,点A在![]() 轴上,点C在
轴上,点C在![]() 轴上,OA=8,OC=6.
轴上,OA=8,OC=6.
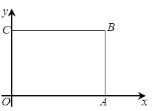

(1)求直线AC的表达式
(2)若直线![]() 与矩形OABC有公共点,求
与矩形OABC有公共点,求![]() 的取值范围;
的取值范围;
(3)若点O与点B位于直线![]() 两侧,直接写出
两侧,直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com