
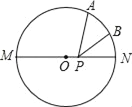
【题目】如图,MN是⊙O的直径,点A是半圆上的三等分点,点B是劣弧AN的中点,点P是直径MN上一动点.若MN=2![]() ,AB=1,则△PAB周长的最小值是( )
,AB=1,则△PAB周长的最小值是( )
A. 2![]() +1 B.
+1 B. ![]() +1 C. 2 D. 3
+1 C. 2 D. 3
【答案】D
【解析】
作点A关于MN的对称点A′,连接A′B,交MN于点P,连接OA′,OA,OB,PA,AA′.所以点A与A′关于MN对称,点A是半圆上的一个三等分点,所以∠A′ON=∠AON=60°,PA=PA′,OA=OA′=![]() ,因为点B是弧AN的中点,所以∠BON=30°,∠A′OB=∠A′ON+∠BON=90°,再由勾股定理求出A′B=2,最后即可求解.
,因为点B是弧AN的中点,所以∠BON=30°,∠A′OB=∠A′ON+∠BON=90°,再由勾股定理求出A′B=2,最后即可求解.

作点A关于MN的对称点A′,连接A′B,交MN于点P,连接OA′,OA,OB,PA,AA′.
∵点A与A′关于MN对称,点A是半圆上的一个三等分点,
∴∠A′ON=∠AON=60°,PA=PA′,
∵点B是弧AN的中点,
∴∠BON=30°,
∴∠A′OB=∠A′ON+∠BON=90°,
又∵OA=OA′=![]() ,
,
∴A′B=2.
∴PA+PB=PA′+PB=A′B=2.
∴△PAB周长的最小值=PA+PB+AB=2+1=3
故选D.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
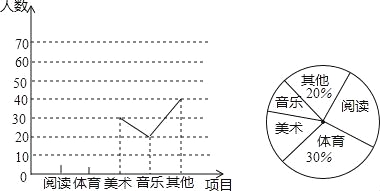
【题目】某学校为了解该校学生的课余活动情况,抽样调查了部分同学,将所得数据处理后,制成折线统计图(部分)和扇形统计图(部分)如下:
(1)在这次研究中,一共调查了 名学生.
(2)补全频数分布折线图;
(3)该校共有2200名学生,估计该校学生中爱好阅读的人数大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:在小学已经学过“正方形的四条边都相等,正方形的四个内角都是直角”,试利用上述知识,并结合已学过的知识解答下列问题:
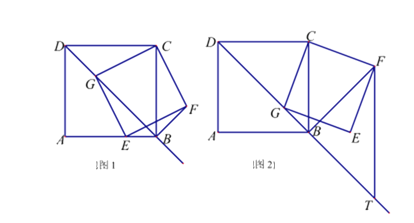
如图1,在正方形ABCD中,G是射线DB上的一个动点(点G不与点D重合),以CG为边向下作正方形CGEF.
(1)当点G在线段BD上时,求证:![]() ;
;
(2)连接BF,试探索:BF,BG与AB的数量关系,并说明理由;
(3)若AB=a(a是常数),如图2,过点F作FT∥BC,交射线DB于点T,问在点G的运动过程中,GT的长度是否会随着G点的移动而变化?若不变,请求出GT的长度;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.
(1)k的值是 ;
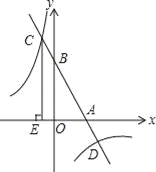
(2)如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y=![]() 图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若
图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若![]() =
=![]() ,则b的值是 .
,则b的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解答问题.
(阅读)例题:求多项式m2 + 2mn+2n2-6n+13的最小值.
解;m2+2mn+2n2-6n+ 13= (m2 +2mn+n2)+ (n2-6n+9)+4= (m+n)2+(n-3)2+4,
∵(m+n)2![]() 0, (n-3)2
0, (n-3)2![]() 0
0
∴多项式m2+2mn+2n2-6n+ 13的最小值是4.
(解答问题)
(1)请写出例题解答过程中因式分解运用的公式是
(2)己知a、b、c是△ABC的三边,且满足a2+b2=l0a+8b-41,求第三边c的取值范围;
(3)求多项式-2x2+4xy-3y2 -3y2-6y+7 的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的____(把你认为正确结论的序号都填上)
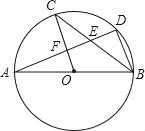
查看答案和解析>>
科目:初中数学 来源: 题型:
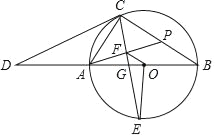
【题目】如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,CE交AB于点G,过点A作AF⊥CE于点F,延长AF交BC于点P.
(Ⅰ)求∠CPA的度数;
(Ⅱ)连接OF,若AC=![]() ,∠D=30°,求线段OF的长.
,∠D=30°,求线段OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
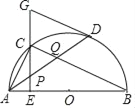
【题目】如图,AB是半圆O的直径,点D是半圆O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.
(1)求证:GP=GD;
(2)求证:P是线段AQ的中点;
(3)连接CD,若CD=2,BC=4,求⊙O的半径和CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且2≤x≤1时,y的最大值为9,则a的值为
A. 1或2 B. ![]() 或
或![]()
C. ![]() D. 1
D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com