
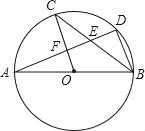
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的____(把你认为正确结论的序号都填上)
【答案】①③④⑤
【解析】
根据圆周角定理、平行线的性质、垂径定理等判断即可.
①∵AB是⊙O的直径,∴∠ADB=90°,∴AD⊥BD,故①正确;
②∵∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角,∴∠AOC≠∠AEC,故②不正确;
③∵OC∥BD,∴∠OCB=∠DBC.
∵OC=OB,∴∠OCB=∠OBC,∴∠OBC=∠DBC,∴BC平分∠ABD,故③正确;
④∵AB是⊙O的直径,∴∠ADB=90°,∴AD⊥BD.
∵OC∥BD,∴∠AFO=90°.
∵点O为圆心,∴AF=DF,故④正确;
⑤由④有,AF=DF.
∵点O为AB中点,∴OF是△ABD的中位线,∴BD=2OF,故⑤正确;
⑥∵△CEF和△BED中,没有相等的边,∴△CEF与△BED不全等,故⑥不正确.
综上可知:其中一定成立的有①③④⑤.
故答案为:①③④⑤.


科目:初中数学 来源: 题型:
【题目】由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负.
如果小王和小张按上述规则各转动转盘一次,则
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个完全相同的标有数字1、2、3、4的小球. 小明从布袋里随机取出一个小球,记下数字为x,小红从布袋里剩下的小球中随机取出一个,记下数字为y. 计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
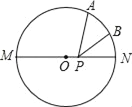
【题目】如图,MN是⊙O的直径,点A是半圆上的三等分点,点B是劣弧AN的中点,点P是直径MN上一动点.若MN=2![]() ,AB=1,则△PAB周长的最小值是( )
,AB=1,则△PAB周长的最小值是( )
A. 2![]() +1 B.
+1 B. ![]() +1 C. 2 D. 3
+1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE,连接OC.
(1)求证:DE是⊙O的切线;
(2)若⊙O半径为4,∠D=30°,求图中阴影部分的面积(结果用含π和根号的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种纪念品,11月份的营业额为2 000元.为扩大销售,12月份该商店对这种纪念品打九折销售,结果销售量增加20件,营业额增加700元.
(1)求这种纪念品11月份的销售单价;
(2)11月份该商店销售这种商品_______件;
(3)若11月份销售这种纪念品获利800元,求12月份销售这种纪念品获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为6的等边![]() 中,
中,![]() 是高
是高![]() 所在直线上的一个动点,连接
所在直线上的一个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,则在点
,则在点![]() 运动的过程中,当线段
运动的过程中,当线段![]() 长度的最小值时,
长度的最小值时,![]() 的长度为__________.
的长度为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com