
【题目】已知边长为6的等边![]() 中,
中,![]() 是高
是高![]() 所在直线上的一个动点,连接
所在直线上的一个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,则在点
,则在点![]() 运动的过程中,当线段
运动的过程中,当线段![]() 长度的最小值时,
长度的最小值时,![]() 的长度为__________.
的长度为__________.

【答案】1.5
【解析】
取BA的中点G,连接EG,证明△EBG≌△FBD,根据全等三角形的性质EG=FD,所以只需要求得EG的最短值就好,根据点到直线的距离垂线段最短,当GE⊥AD时,GE最短.此时在Rt△AGE中可求∠BAD=30°,从而根据直角三角形30°角所对边是斜边的一半可求GE=![]() AG=1.5.
AG=1.5.
解:如图,取BA的中点G,连接EG,

∵△ABC为等边三角形,
∴∠BAC=∠CBA=60°,AB=BC
∵旋转角为60°,
∴∠EBD+∠DBF=60°,
又∵∠EBD+∠EBA=∠CBA=60°,
∴∠DBF=∠ABE,
∵AD是等边△CBA的高,
∴DB=![]() CB,∠BAD=
CB,∠BAD=![]() ×∠BAC=30°,
×∠BAC=30°,
∵G为AB的中点
∴BG=![]() AB,
AB,
∴DB=BG,
又∵EB旋转到BF,
∴BE=BF,
在△EBG和△FBD中,
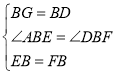 ,
,
∴△EBG≌△FBD(SAS),
∴EG=FD,
根据点到直线的距离,垂线段最短,EG⊥AD时,EG最短,即DF最短,
此时,
∵∠BAD=30°,AG=![]() AB=
AB=![]() ×6=3,
×6=3,
∴EG=![]() AG=
AG=![]() ×3=1. 5,
×3=1. 5,
∴DF=1.5,
故答案为:1.5.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
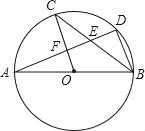
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的____(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
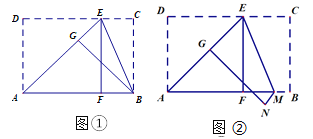
【题目】李刚和常明两人在数学活动课上进行折纸创编活动.李刚拿起一张准备好的长方形纸片对常明说:“我现在折叠纸片(图①),使点D落在AB边的点F处,得折痕AE,再折叠,使点C落在AE边的点G处,此时折痕恰好经过点B,如果AD=![]() ,那么AB长是多少?”常明说;“简单,我会. AB应该是_____”.
,那么AB长是多少?”常明说;“简单,我会. AB应该是_____”.
常明回答完,又对李刚说:“你看我的创编(图②),与你一样折叠,可是第二次折叠时,折痕不经过点B,而是经过了AB边上的M点,如果AD=![]() ,测得EC=3BM,那么AB长是多少?”李刚思考了一会,有点为难,聪明的你,你能帮忙解答吗?AB=_____.
,测得EC=3BM,那么AB长是多少?”李刚思考了一会,有点为难,聪明的你,你能帮忙解答吗?AB=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC∽△DEC,CA=CB,且点E在AB的延长线上.
(1)求证:AE=BD;
(2)求证:△BOE∽△COD;
(3)已知CD=10,BE=5,OD=6,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且2≤x≤1时,y的最大值为9,则a的值为
A. 1或2 B. ![]() 或
或![]()
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,建筑物AB的高为6cm,在其正东方向有个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A、塔项C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() =1.73,精确到0.1m)
=1.73,精确到0.1m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() ,现有两点
,现有两点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,沿三角形的边运动,已知点
同时出发,沿三角形的边运动,已知点![]() 的速度为
的速度为![]() ,点
,点![]() 的速度为
的速度为![]() .当点
.当点![]() 第一次回到点
第一次回到点![]() 时,点
时,点![]() 、
、![]() 同时停止运动,设运动时间为
同时停止运动,设运动时间为![]() .
.
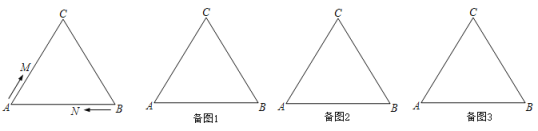
(1)当![]() 为何值时,
为何值时,![]() 、
、![]() 两点重合;
两点重合;
(2)当点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动,
边上运动,![]() 的形状会不断发生变化.
的形状会不断发生变化.
①当![]() 为何值时,
为何值时,![]() 是等边三角形;
是等边三角形;
②当![]() 为何值时,
为何值时,![]() 是直角三角形;
是直角三角形;
(3)若点![]() 、
、![]() 都在
都在![]() 边上运动,当存在以
边上运动,当存在以![]() 为底边的等腰
为底边的等腰![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
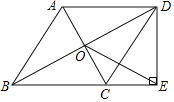
【题目】如图,在四边形ABCD中,AD∥BC,AB=BC,对角线AC、BD交于点O,BD平分∠ABC,过点D作DE⊥BC,交BC的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若DC=2![]() ,AC=4,求OE的长.
,AC=4,求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com