
【题目】如图,△ABC∽△DEC,CA=CB,且点E在AB的延长线上.
(1)求证:AE=BD;
(2)求证:△BOE∽△COD;
(3)已知CD=10,BE=5,OD=6,求OC的长.

【答案】(1)详见解析;(2)详见解析;(3)CO=7.
【解析】
(1)利用相似三角形的性质:对应边的比值相等可证明CE=CD,再根据全等三角形的判定方法可证明△ACE≌△CBD,进而证明AE=BD;
(2)利用有两对角相等的两三角形相似即可证明:△BOE∽△COD.
(3)根据相似三角形的性质解答即可.
证明:(1)∵△ABC∽△DEC,CA=CB,
∴![]()
∴CE=CD,∠ACB=∠ECD,
∴∠ACB+∠BCE=∠ECD+∠BCE,
∴∠ACE=∠BCD,
在△ACE和△BCD中, ,
,
∴△ACE≌△BCD(SAS),
∴AE=BD;
(2)∵△ACE≌△BCD.
∴∠AEC=∠BDC,
∵∠DOC=∠EOB,
∴△COD∽△BOE,
(3)∵△BOE∽△COD.
∴![]() =
=![]() ,
,
∵CD=10,BE=5, OD=6,
∴![]() =
=![]()
∴OE=3
∴CO=CE﹣OE=CD﹣OE=10﹣3=7.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种纪念品,11月份的营业额为2 000元.为扩大销售,12月份该商店对这种纪念品打九折销售,结果销售量增加20件,营业额增加700元.
(1)求这种纪念品11月份的销售单价;
(2)11月份该商店销售这种商品_______件;
(3)若11月份销售这种纪念品获利800元,求12月份销售这种纪念品获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上,如果BC=5,△ABC的面积是10,那么这个正方形的边长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以每秒一个单位的速度沿
出发,以每秒一个单位的速度沿![]() 的方向运动;同时点
的方向运动;同时点![]() 从点
从点![]() 出发,以每秒2个单位的速度沿
出发,以每秒2个单位的速度沿![]() 的方向运动,当其中一点到达终点后两点都停止运动.设两点运动的时间为
的方向运动,当其中一点到达终点后两点都停止运动.设两点运动的时间为![]() 秒.
秒.

(1)当![]() ______时,两点停止运动;
______时,两点停止运动;
(2)当![]() 为何值时,
为何值时,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为6的等边![]() 中,
中,![]() 是高
是高![]() 所在直线上的一个动点,连接
所在直线上的一个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,则在点
,则在点![]() 运动的过程中,当线段
运动的过程中,当线段![]() 长度的最小值时,
长度的最小值时,![]() 的长度为__________.
的长度为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]()
![]() 与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴
与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴![]() 为
为![]() =–1,P为抛物线上第二象限的一个动点.
=–1,P为抛物线上第二象限的一个动点.
(1)求抛物线的解析式并写出其顶点坐标;
(2)当点P的纵坐标为2时,求点P的横坐标;
(3)当点P在运动过程中,求四边形PABC面积最大时的值及此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
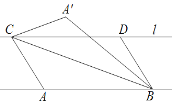
【题目】如图,已知直线l//AB,l与AB之间的距离为2.C、D是直线l上两个动点(点C在D点的左侧),且AB=CD=5.连接AC、BC、BD,将△ABC沿BC折叠得到△A′BC.下列说法:①四边形ABDC的面积始终为10;②当A′与D重合时,四边形ABDC是菱形;③当A′与D不重合时,连接A′、D,则∠CA′D+∠BC A′=180°;④若以A′、C、B、D为顶点的四边形为矩形,则此矩形相邻两边之和为3![]() 或7.其中正确的是( )
或7.其中正确的是( )
A. ①②③④B. ①③④C. ①②④D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com