
【题目】先阅读下面的内容,再解答问题.
(阅读)例题:求多项式m2 + 2mn+2n2-6n+13的最小值.
解;m2+2mn+2n2-6n+ 13= (m2 +2mn+n2)+ (n2-6n+9)+4= (m+n)2+(n-3)2+4,
∵(m+n)2![]() 0, (n-3)2
0, (n-3)2![]() 0
0
∴多项式m2+2mn+2n2-6n+ 13的最小值是4.
(解答问题)
(1)请写出例题解答过程中因式分解运用的公式是
(2)己知a、b、c是△ABC的三边,且满足a2+b2=l0a+8b-41,求第三边c的取值范围;
(3)求多项式-2x2+4xy-3y2 -3y2-6y+7 的最大值.
【答案】(1)完全平方公式;(2)1<c<9;(3)16
【解析】
(1)根据完全平方公式的特点求解;(2)配方可得(a-5)2+(b-4)2=0.求出a,b,可求出第三边取值范围;(3)运用完全平方公式,变形可得-2(x-y)2 -(y+3)2 +16,可求最大值.
解:(1)完全平方公式.
(2)∵a2 +b2 =10a+8b-41,∴a2-10a+25+b2-8b+16=0,
∴(a-5)2+(b-4)2=0.
∵(a-5)2≥0,(b-4)2≥0,∴a=5,b=4.
∴1<c<9.
(3)原式=-2x2+4xy-2y2 -y2-6y-9+16
=-2(x-y)2 -(y+3)2 +16,
∵-2(x-y)2≤0,-(y+3)2≤0,
∴ 多项式-2x2+4xy-3y2-6y+7 的最大值是 16.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
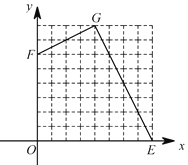
【题目】如图,在平面直角坐标系 ![]() 中,
中,![]() ,
,![]() .
.
①当 ![]() 时,则
时,则![]() ______;
______;
②在图中的网格区域内找一点![]() ,使
,使![]() ,且四边形
,且四边形![]() 被过
被过![]() 点的一条直线分割成两部分后,可以拼成一个正方形,则
点的一条直线分割成两部分后,可以拼成一个正方形,则![]() 点坐标为_______.
点坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程m x2-(m+2)x+2=0(m≠0).
(1)求证:无论m为何值时,这个方程总有两个实数根;
(2)若方程的两个实数根都是整数,求正整数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
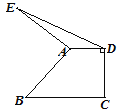
【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于 ( )
A.10 B.11 C.12 D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.

(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是___个单位长度;△AOC与△BOD关于直线对称,则对称轴是___;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是___度;
(2)连结AD,交OC于点E,求∠AEO的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
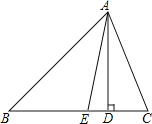
【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=15°,∠B=40°.
(1)求∠C的度数.
(2)若:∠EAD=α,∠B=β,其余条件不变,直接写出用含α,β的式子表示∠C的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com