
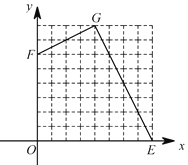
【题目】如图,在平面直角坐标系 ![]() 中,
中,![]() ,
,![]() .
.
①当 ![]() 时,则
时,则![]() ______;
______;
②在图中的网格区域内找一点![]() ,使
,使![]() ,且四边形
,且四边形![]() 被过
被过![]() 点的一条直线分割成两部分后,可以拼成一个正方形,则
点的一条直线分割成两部分后,可以拼成一个正方形,则![]() 点坐标为_______.
点坐标为_______.
【答案】![]()
![]()
【解析】
(1)先利用勾股定理分别计算三边长,再利用勾股定理的逆定理可得:∠FGE=90°;
(2)构建全等三角形:△APF≌△MEP,构建P的位置,根据三角形全等得到正方形.
(1)如图1,连接EF,
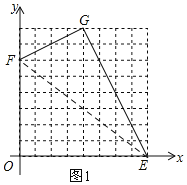
由勾股定理得:FG2=22+42=20,
GE2=42+82=80,
EF2=62+82=100,
∴FG2+GE2=EF2,
∴∠FGE=90°,
故答案为:90°;
(2)如图2,过P作PM⊥x轴于M,当P(7,7),PM为分割线;
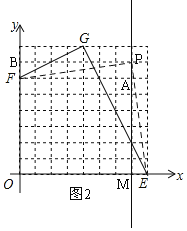
根据格点的长度易得:△APF≌△MEP≌△BFP,
∴∠APF=∠MEP,
∵∠MEP+∠MPE=90°,
∴∠APF+∠MPE=90°,
即∠FPE=90°,
四边形OEPF将△EPM剪下放在△BFP上,构建正方形BOMP;
故答案为:(7,7).


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表:
零花钱数额 | 人数(频数) | 频率 |
| 6 | 0.15 |
| 12 | 0.30 |
| 16 | 0.40 |
|
| 0.10 |
| 2 |
|

请根据以下图表,解答下列问题:
(1)这次被调查的人数共有__________人,![]() __________;
__________;
(2)计算并补全频数分布直方图;
(3)请估计该校1500名学生中每月零花钱数额低于90的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的一边AB为直径作⊙O,交AC,BC于D,E两点,若AB=4,∠BED=120°,点E是BD中点,则图中阴影部分的面积是( )

A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
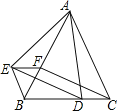
【题目】如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)已知四边形ABCD是矩形,对角线AC和BD相交于点P,若在矩形的上方加一个△DEA,且使DE∥AC,AE∥BD.
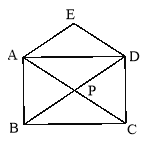
(1)求证:四边形DEAP是菱形;
(2)若AE=CD,求∠DPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为准备参加某市2019年度中小学生机器人竞赛,学校对甲、乙两支机器人制作小队所创作的机器人分别从创意、设计、编程与制作三方面进行量化,各项量化满分100分,根据量化结果择优推荐.它们三项量化得分如下表:
量化项目 | 量化得分 | |
甲队 | 乙队 | |
创意 | 85 | 72 |
设计 | 70 | 66 |
编程与制作 | 64 | 84 |
(1)如果根据三项量化的平均分择优推荐,哪队将被推荐参赛?
(2)根据本次中小学生机器人竞赛的主题要求,如果学校根据创意、设计、编程与制作三项量化得分按![]() 的比例确定每队最后得分的平均分择优推荐,哪队将被推荐参赛?并对另外一队提出合理化的建议.
的比例确定每队最后得分的平均分择优推荐,哪队将被推荐参赛?并对另外一队提出合理化的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用抽样调查的是( )
A.对某地区现有的![]() 名百岁以上老人睡眠时间的调查
名百岁以上老人睡眠时间的调查
B.对“神舟十一号”运载火箭发射前零部件质量情况的调查
C.对某校七年级三班学生视力情况的调查
D.对株洲市民与长沙市民是否了解“株洲南雅实验中学高复班”的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,AC=3 cm,BC=4 cm,以BC为直径作⊙O交AB于点D.
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问当点E在什么位置时,直线ED与⊙O相切?请说明理由.
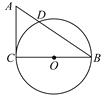
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解答问题.
(阅读)例题:求多项式m2 + 2mn+2n2-6n+13的最小值.
解;m2+2mn+2n2-6n+ 13= (m2 +2mn+n2)+ (n2-6n+9)+4= (m+n)2+(n-3)2+4,
∵(m+n)2![]() 0, (n-3)2
0, (n-3)2![]() 0
0
∴多项式m2+2mn+2n2-6n+ 13的最小值是4.
(解答问题)
(1)请写出例题解答过程中因式分解运用的公式是
(2)己知a、b、c是△ABC的三边,且满足a2+b2=l0a+8b-41,求第三边c的取值范围;
(3)求多项式-2x2+4xy-3y2 -3y2-6y+7 的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com