
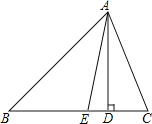
【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=15°,∠B=40°.
(1)求∠C的度数.
(2)若:∠EAD=α,∠B=β,其余条件不变,直接写出用含α,β的式子表示∠C的度数.
【答案】(1)70°;(2)∠C=β+2α.
【解析】
(1)根据三角形的内角和定理求出∠BAD,求出∠BAE,根据角平分线的定义求出∠BAC,即可求出答案;
(2)根据三角形的内角和定理求出∠BAD,求出∠BAE,根据角平分线的定义求出∠BAC,即可求出答案.
(1)∵AD⊥BC,
∴∠ADC=∠ADB=90°,
∵∠B=40°,
∴∠BAD=90°-40°=50°,
∵∠EAD=15°,
∴∠BAE=50°-15°=35°,
∵AE平分∠BAC,
∴∠CAE=∠BAE=![]() ∠BAC=35°,
∠BAC=35°,
∴∠BAC=70°,
∴∠C=180°-∠BAC-∠B=180°-70°-40°=70°;
(2)∵AD⊥BC,
∴∠ADC=∠ADB=90°,
∵∠B=β,
∴∠BAD=90°-β,
∵∠EAD=α,
∴∠BAE=90°-β-α,
∵AE平分∠BAC,
∴∠CAE=∠BAE=![]() ∠BAC=90°-β-α,
∠BAC=90°-β-α,
∴∠BAC=180°-2β-2α,
∴∠C=180°-∠BAC-∠B=180°-(180°-2β-2α)-β=β+2α.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解答问题.
(阅读)例题:求多项式m2 + 2mn+2n2-6n+13的最小值.
解;m2+2mn+2n2-6n+ 13= (m2 +2mn+n2)+ (n2-6n+9)+4= (m+n)2+(n-3)2+4,
∵(m+n)2![]() 0, (n-3)2
0, (n-3)2![]() 0
0
∴多项式m2+2mn+2n2-6n+ 13的最小值是4.
(解答问题)
(1)请写出例题解答过程中因式分解运用的公式是
(2)己知a、b、c是△ABC的三边,且满足a2+b2=l0a+8b-41,求第三边c的取值范围;
(3)求多项式-2x2+4xy-3y2 -3y2-6y+7 的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的对角线AC=8![]() ,BD=6
,BD=6![]() ,且
,且![]() ,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________.
,P、Q、R、S分别是AB、BC、CD、DA的中点,则PR2+QS2的值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接安顺市文明城市创建工作,某校八年一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动,成绩分为A、B、C、D四个等级,并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息,解答下列各题:
(1)求八年一班共有多少人;
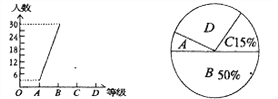
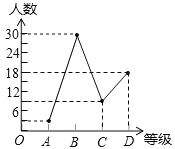
(2)补全折线统计图;
(3)在扇形统计图中等极为“D”的部分所占圆心角的度数为________;
(4)若等级A为优秀,求该班的优秀率.
【答案】(1)60;(2)补图见解析;(3)108°;(4)5%.
【解析】(1)用B等人数除以其所占的百分比即可得到总人数;
(2)用求得的总人数乘以C等所占的百分比即可得到C等的人数,总人数减去A、C等的人数即可求得D等的人数;
(3)用D等的人数除以总人数乘以360°即可得到答案;
(4)用A等的人数除以总人数乘以100%即可得到答案. 解答:
解:(1)30÷50%=60(人)
∴八年级一共有60人。
(2)等级为“C”的人数为60×15%=9(人).
等级为“D”的人数为603309=18(人).
补全折线统计图如下。
(3)等极为“D”的部分所占圆心角的度数为![]() ×360°=108°,
×360°=108°,
故答案为:108°.
(4)该班的优秀率![]() ×100%=5%.
×100%=5%.
∴该班的优秀率为5%.
点睛:本题考查统计相关知识.利用拆线图与扇形图得出相关信息是解题的关键.
【题型】解答题
【结束】
25
【题目】已知抛物线y=ax2+bx+c经过A(﹣1,0),B(3,0),C(0,3)三点,直线L是抛物线的对称轴.
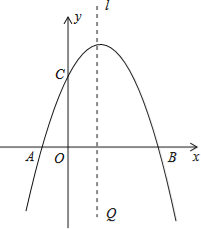
(1)求抛物线的函数关系式;
(2)求抛物线的顶点坐标;
(3)设P点是直线L上的一个动点,当△PAC的周长最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进45件A商品和20件B商品共用了800元,购进60件A商品和35件B商品共用了1100元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购进B商品的件数比购进A商品件数的2倍少4件,如果需要购进A、B两种商品的总件数不少于32件,且该商店购进A、B两种商品的总费用不超过296元,那么该商店有几种购进方案?并写出所有可能的购进方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=x2+bx+c的图象过点A(1,0)和C(0,﹣3)
(1)求这个二次函数的解析式;
(2)如果这个二次函数的图象与x轴的另一个交点为B,求线段AB的长.
(3)在这条抛物线上是否存在一点P,使△ABP的面积为8?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
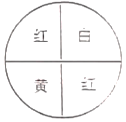
【题目】如图,小华蒙上眼睛投飞镖且中目标(转盘技等分成4个扇形,投在边线上忽略)(直接填写答案)
(1)击中红色区域的概率是 .
(2)击中白色区域的概率是 .
(3)没有击中黄色区域的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市市民2018年乘坐公交车的每人月均花费情况,相关部门随机调查了1000人的相关信息,并绘制了如图所示的频数直方图,根据图中提供的信息,有下列说法(每组值包括最低值,不包括最高值):①乘坐公交车的月均花费在60元~80元的人数最多;②月均花费在160元(含160元)以上的人数占所调查总人数的10%;③在所调查的1000人中,至少有一半以上的人的月均花费超过75元;④为了让市民享受更多的优惠,相关部门拟确定一个折扣标准,计划使30%左右的人获得优惠,那么可以是乘坐公交车的月均花费达到100元(含100元)以上的人享受折扣.

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com