练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，，结论：①；②；③；④，其中正确的是有（ ）

    A.1个B.2个C.3个D.4个

    【答案】C

    【解析】

    根据已知的条件，可由AAS判定△AEB≌△AFC，进而可根据全等三角形得出的结论来判断各选项是否正确．

    解：如图：

    在△AEB和△AFC中，有

    ，

    ∴△AEB≌△AFC；（AAS）

    ∴∠FAM=∠EAN，

    ∴∠EAN-∠MAN=∠FAM-∠MAN，

    即∠EAM=∠FAN；（故③正确）

    又∵∠E=∠F=90°，AE=AF，

    ∴△EAM≌△FAN；（ASA）

    ∴EM=FN；（故①正确）

    由△AEB≌△AFC知：∠B=∠C，AC=AB；

    又∵∠CAB=∠BAC，

    ∴△ACN≌△ABM；（故④正确）

    由于条件不足，无法证得②CD=DN；

    故正确的结论有：①③④；

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列调查中，最适合采用抽样调查的是（ ）

    A.对某地区现有的名百岁以上老人睡眠时间的调查

    B.对“神舟十一号”运载火箭发射前零部件质量情况的调查

    C.对某校七年级三班学生视力情况的调查

    D.对株洲市民与长沙市民是否了解“株洲南雅实验中学高复班”的调查

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列抽样调查较为科学的是（ ）

    为了解电饭锅的米饭是否熟了，小明从中任意取出一小匙米饭进行品尝

    为了解全区域市居民的生活水平，小华在区政府机关部分抽取了人做调查

    为了解某初级中学生的平均体重，小军在七至九年级各抽名学生进行调查

    为了解重庆市2018年的平均气温，小琪上网查询了2018年12月份各天的气温情况

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先阅读下面的内容，再解答问题．

    （阅读）例题：求多项式m2 + 2mn+2n2-6n+13的最小值．

    解；m2+2mn+2n2-6n+ 13= (m2 +2mn+n2)+ (n2-6n+9)+4= (m+n)2+(n-3)2+4，

    ∵(m+n)20, (n-3)20

    ∴多项式m2+2mn+2n2-6n+ 13的最小值是4.

    （解答问题）

    （1）请写出例题解答过程中因式分解运用的公式是

    （2）己知a、b、c是△ABC的三边，且满足a2+b2=l0a+8b-41，求第三边c的取值范围；

    （3）求多项式－2x2＋4xy－3y2 －3y2－6y＋7 的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1所示，将一个边长为2的正方形ABCD和一个长为2，宽为1的长方形CEFD拼在一起，构成一个大的长方形ABEF，现将小长方形CEFD绕点C顺时针旋转至CE′F′D′，旋转角为α．

    （1）当边CD′恰好经过EF的中点H时，求旋转角α的大小；

    （2）如图2，G为BC中点，且0°＜α＜90°，求证：GD′=E′D；

    （3）小长方形CEFD绕点C顺时针旋转一周的过程中，△DCD′与△BCD′能否全等？若能，直接写出旋转角α的大小；若不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CA⊥AB，垂足为 A，AB＝24，AC＝12，射线 BM⊥AB，垂足为 B， 一动点 E 从 A点出发以 3 厘米/秒沿射线 AN 运动，点 D 为射线 BM 上一动点， 随着 E 点运动而运动，且始终保持 ED＝CB，当点 E 经过______秒时，△DEB 与△BCA 全等．

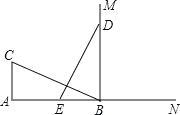
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，小红用一张长方形纸片ABCD进行折纸，已知该纸片宽AB为8cm，长BC为10cm.当小红折叠时，顶点D落在BC边上的点F处（折痕为AE）.

    (1)求BF的长；(2)求EC的长.

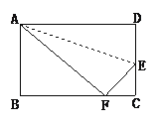
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知四边形ABCD的对角线AC=8，BD=6，且，P、Q、R、S分别是AB、BC、CD、DA的中点，则PR2+QS2的值是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，二次函数y=x2+bx+c的图象过点A（1，0）和C（0，﹣3）

    （1）求这个二次函数的解析式；

    （2）如果这个二次函数的图象与x轴的另一个交点为B，求线段AB的长．

    （3）在这条抛物线上是否存在一点P，使△ABP的面积为8？若存在，求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案