
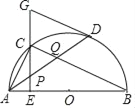
【题目】如图,AB是半圆O的直径,点D是半圆O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.
(1)求证:GP=GD;
(2)求证:P是线段AQ的中点;
(3)连接CD,若CD=2,BC=4,求⊙O的半径和CE的长.
【答案】(1)证明见解析;(2)证明见解析;(3)半径为![]() ;CE=
;CE=![]() ;
;
【解析】
(1)结合切线的性质以及已知得出∠GPD=∠GDP,进而得出答案;
(2)利用圆周角定理得出PA,PC,PQ的数量关系进而得出答案;
(3)直接利用勾股定理结合三角形面积进而得出答案.
(1)证明:连接OD,则OD⊥GD,∠OAD=∠ODA,
∵∠ODA+∠GDP=90°,∠EAP+∠GPD=∠EPA+∠EAP=90°,
∴∠GPD=∠GDP;
∴GP=GD;
(2)证明:∵AB为直径,
∴∠ACB=90°,
∵CE⊥AB于E,
∴∠CEB=90°,
∴∠ACE+∠ECB=∠ABC+∠ECB=90°,
∴∠ACE=∠ABC=∠CAP,
∴PC=PA,
∵∠ACB=90°,
∴∠CQA+∠CAP=∠ACE+∠PCQ=90°,
∴∠PCQ=∠CQA,
∴PC=PQ,
∴PA=PQ,即P为Rt△ACQ斜边AQ的中点;
(3)连接CD,
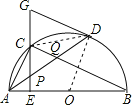
∵弧AC=弧CD,
∴CD=AC,
∵CD=2,
∴AC=2,
∵∠ACB=90°,
∴AB=![]() =
=![]() ,
,
故⊙O的半径为![]() ,
,
∵CE×AB=AC×BC,
∴![]() CE=2×4,
CE=2×4,
∴CE=![]() .
.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinxcosy+cosxsiny.
据此判断下列等式成立的是 (写出所有正确的序号)
①cos(﹣60°)=﹣![]() ;
;
②sin75°=![]() ;
;
③sin2x=2sinxcosx;
④sin(x﹣y)=sinxcosy﹣cosxsiny.
查看答案和解析>>
科目:初中数学 来源: 题型:
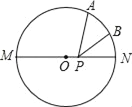
【题目】如图,MN是⊙O的直径,点A是半圆上的三等分点,点B是劣弧AN的中点,点P是直径MN上一动点.若MN=2![]() ,AB=1,则△PAB周长的最小值是( )
,AB=1,则△PAB周长的最小值是( )
A. 2![]() +1 B.
+1 B. ![]() +1 C. 2 D. 3
+1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
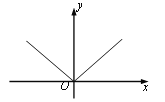
【题目】数学概念:百度百科上这样定义绝对值函数:y=│x│=![]()
并给出了函数的图像(如图).
方法迁移
借鉴研究正比例函数y=kx与一次函数y=kx+b(k,b是常数,且k≠0)之间关系的经验,我们来研究函数y=│x+a│(a是常数)的图像与性质.
“从‘1’开始”
我们尝试从特殊到一般,先研究当a=1时的函数y=│x+1│.
按照要求完成下列问题:
(1)观察该函数表达式,直接写出y的取值范围;
(2)通过列表、描点、画图,在平面直角坐标系中画出该函数的图像.
“从‘1’到一切”
(3)继续研究当a的值为-2,-![]() ,2,3,…时函数y=│x+a│的图像与性质,
,2,3,…时函数y=│x+a│的图像与性质,
尝试总结:
①函数y=│x+a│(a≠0)的图像怎样由函数y=│x│的图像平移得到?
②写出函数y=│x+a│的一条性质.
知识应用
(4)已知A(x1,y1),B(x2,y2)是函数y=│x+a│的图像上的任意两点,且满足x1<x2≤-1时, y1>y2,则a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种纪念品,11月份的营业额为2 000元.为扩大销售,12月份该商店对这种纪念品打九折销售,结果销售量增加20件,营业额增加700元.
(1)求这种纪念品11月份的销售单价;
(2)11月份该商店销售这种商品_______件;
(3)若11月份销售这种纪念品获利800元,求12月份销售这种纪念品获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
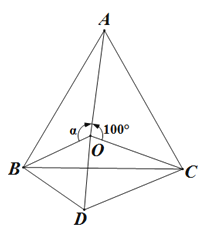
【题目】如图,点O是等边△ABC内一点,∠AOC=100°,∠AOB=α,以OB为边作等边△BOD,连接CD.
(1)求证:△ABO≌△CBD;
(2)当α=150°时,试判断△COD的形状,并说明理由;
(3)探究:当α为多少度时△COD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1的两个长方形可以按不同的形式拼成图2和图3两个图形.
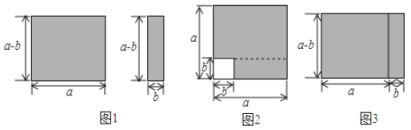
(1)在图2中的阴影部分面积![]() 可表示为 ,在图3中的阴影部分的面积
可表示为 ,在图3中的阴影部分的面积![]() 可表示为 ,由这两个阴影部分的面积得到的一个等式是( )
可表示为 ,由这两个阴影部分的面积得到的一个等式是( )
A. ![]()
B. ![]()
C. ![]()
(2)根据你得到的等式解决下面的问题:
①计算:![]() ;
;
②解方程:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com