
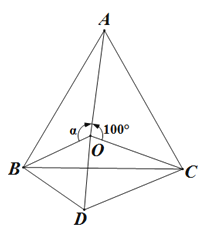
【题目】如图,点O是等边△ABC内一点,∠AOC=100°,∠AOB=α,以OB为边作等边△BOD,连接CD.
(1)求证:△ABO≌△CBD;
(2)当α=150°时,试判断△COD的形状,并说明理由;
(3)探究:当α为多少度时△COD是等腰三角形?
【答案】(1)详见解析;(2)直角三角形,理由详见解析;(3)当α为100°、130°、160°时,△COD是等腰三角形.
【解析】
(1)由于 △ABC和△OBD都是等边三角形,可得BA=BC,BO=BD,由角推出∠ABO=∠CBD,即可证明△ABO≌△CBD.
(2)由△ABO≌△CBD,可得∠BDC=150°,由于∠BDO=60°,即可推出∠CDO的度数为90°,即可证明为直角三角形.
(3)分三类讨论:①要使CO=CD, ②要使OC=OD,③要使OD=CD.
(1)解:(1)∵△ABC和△OBD都是等边三角形,
∴BA=BC,BO=BD,
∵∠ABC=∠OBD=60°
∴∠ABO=∠CBD,
∴△ABO≌△CBD(SAS).
(2)直角三角形;
理由:∵△ABO≌△CBD
∴∠BDC=∠AOB=150°
又∵∠ODB=∠OBD=60°
∴∠CDO=150°-60°=90°
∴△COD是直角三角形.
(3)①要使CO=CD,需∠COD=∠CDO,
∴200°-α = α-60°,
∴α=130°;
②要使OC=OD,需∠OCD=∠CDO,
∴2(α-60°)=180°-(200°-α),
∴α=100°;
③要使OD=CD,需∠OCD=∠COD,
∴2(200°-α)=180°-(α -60°),
∴α=160°.
所以当α为100°、130°、160°时,△COD是等腰三角形.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
【题目】我们知道:在小学已经学过“正方形的四条边都相等,正方形的四个内角都是直角”,试利用上述知识,并结合已学过的知识解答下列问题:
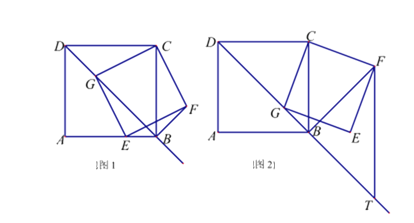
如图1,在正方形ABCD中,G是射线DB上的一个动点(点G不与点D重合),以CG为边向下作正方形CGEF.
(1)当点G在线段BD上时,求证:![]() ;
;
(2)连接BF,试探索:BF,BG与AB的数量关系,并说明理由;
(3)若AB=a(a是常数),如图2,过点F作FT∥BC,交射线DB于点T,问在点G的运动过程中,GT的长度是否会随着G点的移动而变化?若不变,请求出GT的长度;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
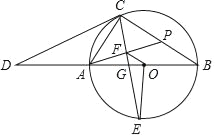
【题目】如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,CE交AB于点G,过点A作AF⊥CE于点F,延长AF交BC于点P.
(Ⅰ)求∠CPA的度数;
(Ⅱ)连接OF,若AC=![]() ,∠D=30°,求线段OF的长.
,∠D=30°,求线段OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
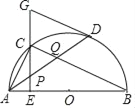
【题目】如图,AB是半圆O的直径,点D是半圆O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.
(1)求证:GP=GD;
(2)求证:P是线段AQ的中点;
(3)连接CD,若CD=2,BC=4,求⊙O的半径和CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=AC=20 cm.动点P,Q分别从A,B两点同时出发,沿三角形的边匀速运动.已知点P,点Q的速度都是2 cm/s,当点P第一次到达B点时,P,Q两点同时停止运动.设点P的运动时间为t(s).
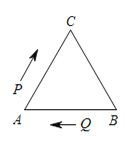
(1)∠A=______度;
(2)当0<t<10,且△APQ为直角三角形时,求t的值;
(3)当△APQ为等边三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
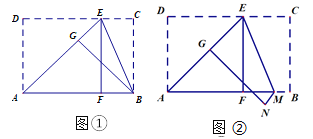
【题目】李刚和常明两人在数学活动课上进行折纸创编活动.李刚拿起一张准备好的长方形纸片对常明说:“我现在折叠纸片(图①),使点D落在AB边的点F处,得折痕AE,再折叠,使点C落在AE边的点G处,此时折痕恰好经过点B,如果AD=![]() ,那么AB长是多少?”常明说;“简单,我会. AB应该是_____”.
,那么AB长是多少?”常明说;“简单,我会. AB应该是_____”.
常明回答完,又对李刚说:“你看我的创编(图②),与你一样折叠,可是第二次折叠时,折痕不经过点B,而是经过了AB边上的M点,如果AD=![]() ,测得EC=3BM,那么AB长是多少?”李刚思考了一会,有点为难,聪明的你,你能帮忙解答吗?AB=_____.
,测得EC=3BM,那么AB长是多少?”李刚思考了一会,有点为难,聪明的你,你能帮忙解答吗?AB=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且2≤x≤1时,y的最大值为9,则a的值为
A. 1或2 B. ![]() 或
或![]()
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 、
、![]() 、
、![]() .
.
(1)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() (其中
(其中![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的对应点)并直接写出
的对应点)并直接写出![]() 点的坐标为 .
点的坐标为 .
(2)若直线![]() 经过点
经过点![]() 且与
且与![]() 轴平行,则点
轴平行,则点![]() 关于直线
关于直线![]() 的对称点的坐标为 .
的对称点的坐标为 .
(3)在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 最大,则点
最大,则点![]() 的坐标为 .
的坐标为 .
(4)第一象限有一点![]() ,在
,在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最短,画出最短路径,保留作图迹.
最短,画出最短路径,保留作图迹.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com