
【题目】如图,在平面直角坐标系中,![]() 、
、![]() 、
、![]() .
.
(1)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() (其中
(其中![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的对应点)并直接写出
的对应点)并直接写出![]() 点的坐标为 .
点的坐标为 .
(2)若直线![]() 经过点
经过点![]() 且与
且与![]() 轴平行,则点
轴平行,则点![]() 关于直线
关于直线![]() 的对称点的坐标为 .
的对称点的坐标为 .
(3)在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 最大,则点
最大,则点![]() 的坐标为 .
的坐标为 .
(4)第一象限有一点![]() ,在
,在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最短,画出最短路径,保留作图迹.
最短,画出最短路径,保留作图迹.
科目:初中数学 来源: 题型:
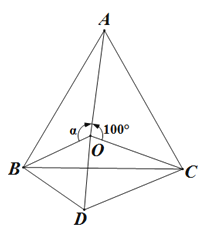
【题目】如图,点O是等边△ABC内一点,∠AOC=100°,∠AOB=α,以OB为边作等边△BOD,连接CD.
(1)求证:△ABO≌△CBD;
(2)当α=150°时,试判断△COD的形状,并说明理由;
(3)探究:当α为多少度时△COD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点C'处,连接C'D交AB于点E,连接BC',当△BC'D是直角三角形时,DE的长为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1的两个长方形可以按不同的形式拼成图2和图3两个图形.
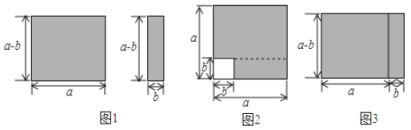
(1)在图2中的阴影部分面积![]() 可表示为 ,在图3中的阴影部分的面积
可表示为 ,在图3中的阴影部分的面积![]() 可表示为 ,由这两个阴影部分的面积得到的一个等式是( )
可表示为 ,由这两个阴影部分的面积得到的一个等式是( )
A. ![]()
B. ![]()
C. ![]()
(2)根据你得到的等式解决下面的问题:
①计算:![]() ;
;
②解方程:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
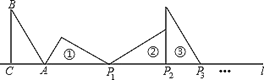
【题目】如图,在△ABC中,∠ACB=![]() ,∠B=
,∠B=![]() ,AC=1,BC=
,AC=1,BC=![]() ,AB=2,AC在直线l上,将△ABC绕点A顺时针转到位置①可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+
,AB=2,AC在直线l上,将△ABC绕点A顺时针转到位置①可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+![]() …,按此顺序继续旋转,得到点P2016,则AP2016=( )
…,按此顺序继续旋转,得到点P2016,则AP2016=( )
A. 2016+671![]() B. 2016+672
B. 2016+672![]()
C. 2017+671![]() D. 2017+672
D. 2017+672![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
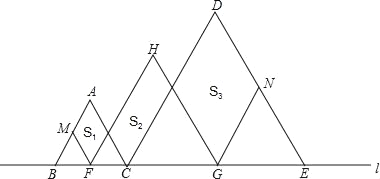
【题目】如图,在直线l上摆放着三个三角形:△ABC、△HFG、△DCE,已知BC=![]() CE,F、G分别是BC、CE的中点,FM∥AC∥HG∥DE,GN∥DC∥HF∥AB.设图中三个四边形的面积依次是S1,S2,S3,若S1+S3=20,则S1=_____,S2=_____.
CE,F、G分别是BC、CE的中点,FM∥AC∥HG∥DE,GN∥DC∥HF∥AB.设图中三个四边形的面积依次是S1,S2,S3,若S1+S3=20,则S1=_____,S2=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
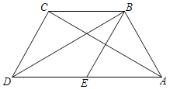
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,AB=2,求菱形BCDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点![]() 将
将![]() 的弦
的弦![]() 和
和![]() 分成的四条线段
分成的四条线段![]() ,
,![]() ,
,![]() ,
,![]() 的长度恰好是四个互不相同的正整数,则称点
的长度恰好是四个互不相同的正整数,则称点![]() 为
为![]() 的”整分点”.现已知
的”整分点”.现已知![]() 是半径为
是半径为![]() 的
的![]() 上一点,则在半径
上一点,则在半径![]() 上有________个不同的整分点.
上有________个不同的整分点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com