
【题目】如图1的两个长方形可以按不同的形式拼成图2和图3两个图形.
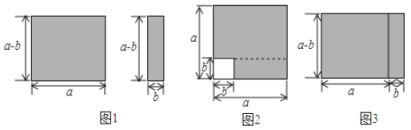
(1)在图2中的阴影部分面积![]() 可表示为 ,在图3中的阴影部分的面积
可表示为 ,在图3中的阴影部分的面积![]() 可表示为 ,由这两个阴影部分的面积得到的一个等式是( )
可表示为 ,由这两个阴影部分的面积得到的一个等式是( )
A. ![]()
B. ![]()
C. ![]()
(2)根据你得到的等式解决下面的问题:
①计算:![]() ;
;
②解方程:![]()
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
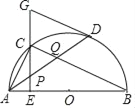
【题目】如图,AB是半圆O的直径,点D是半圆O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.
(1)求证:GP=GD;
(2)求证:P是线段AQ的中点;
(3)连接CD,若CD=2,BC=4,求⊙O的半径和CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且2≤x≤1时,y的最大值为9,则a的值为
A. 1或2 B. ![]() 或
或![]()
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,建筑物AB的高为6cm,在其正东方向有个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A、塔项C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() =1.73,精确到0.1m)
=1.73,精确到0.1m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() 、
、![]() 分别与圆相交于
分别与圆相交于![]() 、
、![]() ,那么下列等式中一定成立的是( )
,那么下列等式中一定成立的是( )
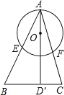
A. AEBF=AFCF B. AEAB=AOAD'
C. AEAB=AFAC D. AEAF=AOAD
查看答案和解析>>
科目:初中数学 来源: 题型:
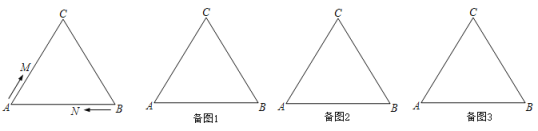
【题目】如图,在等边![]() 中,
中,![]() ,现有两点
,现有两点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,沿三角形的边运动,已知点
同时出发,沿三角形的边运动,已知点![]() 的速度为
的速度为![]() ,点
,点![]() 的速度为
的速度为![]() .当点
.当点![]() 第一次回到点
第一次回到点![]() 时,点
时,点![]() 、
、![]() 同时停止运动,设运动时间为
同时停止运动,设运动时间为![]() .
.
(1)当![]() 为何值时,
为何值时,![]() 、
、![]() 两点重合;
两点重合;
(2)当点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动,
边上运动,![]() 的形状会不断发生变化.
的形状会不断发生变化.
①当![]() 为何值时,
为何值时,![]() 是等边三角形;
是等边三角形;
②当![]() 为何值时,
为何值时,![]() 是直角三角形;
是直角三角形;
(3)若点![]() 、
、![]() 都在
都在![]() 边上运动,当存在以
边上运动,当存在以![]() 为底边的等腰
为底边的等腰![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 、
、![]() 、
、![]() .
.
(1)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() (其中
(其中![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的对应点)并直接写出
的对应点)并直接写出![]() 点的坐标为 .
点的坐标为 .
(2)若直线![]() 经过点
经过点![]() 且与
且与![]() 轴平行,则点
轴平行,则点![]() 关于直线
关于直线![]() 的对称点的坐标为 .
的对称点的坐标为 .
(3)在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 最大,则点
最大,则点![]() 的坐标为 .
的坐标为 .
(4)第一象限有一点![]() ,在
,在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最短,画出最短路径,保留作图迹.
最短,画出最短路径,保留作图迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将等腰直角三角形ABC(AB=AC,∠BAC=90°)和等腰直角三角形DEF(DE=DF,∠EDF=90°)按图1摆放,点D在BC边的中点上,点A在DE上.
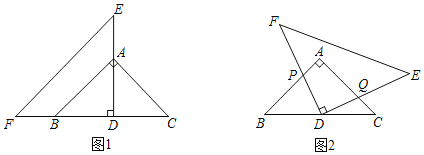
(1)填空:AB与EF的位置关系是 ;
(2)△DEF绕点D按顺时针方向转动至图2所示位置时,DF,DE分别交AB,AC于点P,Q,求证:∠BPD+∠DQC=180°;
(3)如图2,在△DEF绕点D按顺时针方向转动过程中,始终点P不到达A点,△ABC的面积记为S1,四边形APDQ的面积记为S2,那么S1与S2之间是否存在不变的数量关系?若存在,请写出它们之间的数量关系并证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)在一个不透明的袋中装有3 个完全相同的小球,上面分别标号为1、2、3,从中随机摸出两个小球,并用球上的数字组成一个两位数.
(1)求组成的两位数是奇数的概率;
(2)小明和小华做游戏,规则是:若组成的两位数是4的倍数,小明得3分,否则小华得3分,你认为该游戏公平吗?说明理由;若不公平,请修改游戏规则,使游戏公平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com