
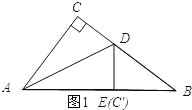
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点C'处,连接C'D交AB于点E,连接BC',当△BC'D是直角三角形时,DE的长为_________.

【答案】![]() 或
或![]()
【解析】试题分析:如图1所示;点E与点C′重合时.在Rt△ABC中,BC=![]() =4.由翻折的性质可知;AE=AC=3、DC=DE.则EB=2.设DC=ED=x,则BD=4﹣x.在Rt△DBE中,DE2+BE2=DB2,即x2+22=(4﹣x)2.解得:x=
=4.由翻折的性质可知;AE=AC=3、DC=DE.则EB=2.设DC=ED=x,则BD=4﹣x.在Rt△DBE中,DE2+BE2=DB2,即x2+22=(4﹣x)2.解得:x=![]() .∴DE=
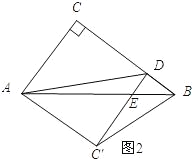
.∴DE=![]() .如图2所示:∠EDB=90时.由翻折的性质可知:AC=AC′,∠C=∠C′=90°.∵∠C=∠C′=∠CDC′=90°,∴四边形ACDC′为矩形.又∵AC=AC′,∴四边形ACDC′为正方形.∴CD=AC=3.∴DB=BC﹣DC=4﹣3=1.∵DE∥AC,∴△BDE∽△BCA.∴
.如图2所示:∠EDB=90时.由翻折的性质可知:AC=AC′,∠C=∠C′=90°.∵∠C=∠C′=∠CDC′=90°,∴四边形ACDC′为矩形.又∵AC=AC′,∴四边形ACDC′为正方形.∴CD=AC=3.∴DB=BC﹣DC=4﹣3=1.∵DE∥AC,∴△BDE∽△BCA.∴![]() ,即
,即![]() .解得:DE=
.解得:DE=![]() .点D在CB上运动,∠DBC′<90°,故∠DBC′不可能为直角.
.点D在CB上运动,∠DBC′<90°,故∠DBC′不可能为直角.


科目:初中数学 来源: 题型:
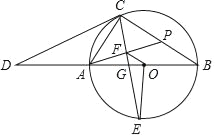
【题目】如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,CE交AB于点G,过点A作AF⊥CE于点F,延长AF交BC于点P.
(Ⅰ)求∠CPA的度数;
(Ⅱ)连接OF,若AC=![]() ,∠D=30°,求线段OF的长.
,∠D=30°,求线段OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且2≤x≤1时,y的最大值为9,则a的值为
A. 1或2 B. ![]() 或
或![]()
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提倡绿色出行,某公司在我区![]() 、
、![]() 两个街区分别投放了一批“共享汽车”,“共享汽车”有甲、乙不同款型.
两个街区分别投放了一批“共享汽车”,“共享汽车”有甲、乙不同款型.
(1)该公司在我区![]() 街区早期试点时共投放甲、乙两种型号的“共享汽车”各20辆,投放成本共计划110万,其中甲型汽车的成本单价比乙型汽车少0.5万元,求甲、乙两型“共享汽车”的单价各是多少?
街区早期试点时共投放甲、乙两种型号的“共享汽车”各20辆,投放成本共计划110万,其中甲型汽车的成本单价比乙型汽车少0.5万元,求甲、乙两型“共享汽车”的单价各是多少?
(2)该公司采取了如下的投放方式: ![]() 街区每2000人投放
街区每2000人投放![]() 辆“共享汽车”,
辆“共享汽车”,![]() 街区每2000人投放
街区每2000人投放![]() 辆“共享汽车”,按照这种设放方式,
辆“共享汽车”,按照这种设放方式,![]() 街区共投放150辆,
街区共投放150辆,![]() 街区共投放120辆,如果两个街区共有6万人,试求
街区共投放120辆,如果两个街区共有6万人,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,建筑物AB的高为6cm,在其正东方向有个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A、塔项C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() =1.73,精确到0.1m)
=1.73,精确到0.1m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() 、
、![]() 分别与圆相交于
分别与圆相交于![]() 、
、![]() ,那么下列等式中一定成立的是( )
,那么下列等式中一定成立的是( )
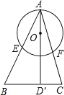
A. AEBF=AFCF B. AEAB=AOAD'
C. AEAB=AFAC D. AEAF=AOAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 、
、![]() 、
、![]() .
.
(1)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() (其中
(其中![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的对应点)并直接写出
的对应点)并直接写出![]() 点的坐标为 .
点的坐标为 .
(2)若直线![]() 经过点
经过点![]() 且与
且与![]() 轴平行,则点
轴平行,则点![]() 关于直线
关于直线![]() 的对称点的坐标为 .
的对称点的坐标为 .
(3)在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 最大,则点
最大,则点![]() 的坐标为 .
的坐标为 .
(4)第一象限有一点![]() ,在
,在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最短,画出最短路径,保留作图迹.
最短,画出最短路径,保留作图迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.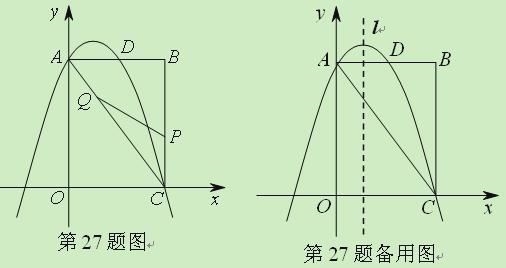
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com